题目内容
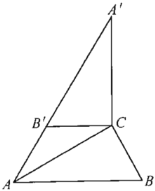
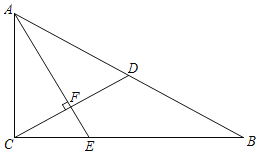
【题目】如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD于点F,交CB于点E,且∠EAB=∠DCB.
(1)求∠B的度数:
(2)求证:BC=3CE.
【答案】(1)∠B=30°;(2)详见解析.
【解析】
(1)根据余角的性质得到∠ECF=∠CAF,求得∠CAD=2∠DCB,由CD是斜边AB上的中线,得到CD=BD,推出∠CAB=2∠B,于是得到结论;
(2)根据直角三角形的性质即可得到结论.
解:(1)∵AE⊥CD,
∴∠AFC=∠ACB=90°,
∴∠CAF+∠ACF=∠ACF+∠ECF=90°,
∴∠ECF=∠CAF,
∵∠EAD=∠DCB,
∴∠CAD=2∠DCB,
∵CD是斜边AB上的中线,
∴CD=BD,
∴∠B=∠DCB,
∴∠CAB=2∠B,
∵∠B+∠CAB=90°,
∴∠B=30°;
(2)∵∠B=∠BAE=∠CAE=30°,
∴AE=BE,CE=![]() AE,
AE,
∴BC=3CE.

练习册系列答案
相关题目