题目内容
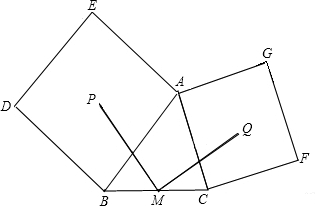
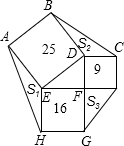
如图，正方形ABDE、CDFI、EFGH的面积分别为25、9、16，△AEH、△BDC、△GFI的面积分别为S1、S2、S3，则S1+S2+S3=________．
18
分析：正方形ABDE、CDFI、EFGH的面积分别为25、9、16，故直角三角形的三边分别为5、4、3，通过求△DEF的面积求出△BDC，△GFI，△AEH的面积即可．
解答：∵DF=DC，DE=DB，且∠EDF+∠BDC=180°，
根据三角形的面积公式得S△AHE=S△DEF，
同理：S△BDC=S△GFI=S△DEF，
S△AHE+S△BDC+S△GFI=S1+S2+S3=3×S△DEF，
S△DEF=
×3×4=6，
∴S1+S2+S3=18．
故答案为：18．
点评：本题考查了正方形各边相等，且各内角等于直角的性质，考查了三角形面积的计算，解本题的关键是找到：S△AHE+S△BDC+S△GFI=3×S△DEF．
分析：正方形ABDE、CDFI、EFGH的面积分别为25、9、16，故直角三角形的三边分别为5、4、3，通过求△DEF的面积求出△BDC，△GFI，△AEH的面积即可．
解答：∵DF=DC，DE=DB，且∠EDF+∠BDC=180°，
根据三角形的面积公式得S△AHE=S△DEF，
同理：S△BDC=S△GFI=S△DEF，
S△AHE+S△BDC+S△GFI=S1+S2+S3=3×S△DEF，
S△DEF=
×3×4=6，∴S1+S2+S3=18．
故答案为：18．
点评：本题考查了正方形各边相等，且各内角等于直角的性质，考查了三角形面积的计算，解本题的关键是找到：S△AHE+S△BDC+S△GFI=3×S△DEF．
练习册系列答案
相关题目
如图，正方形ABDE、CDFI、EFGH的面积分别为25、9、16，△AEH、△BDC、△GFI的面积分别为S1、S2、S3，则S1+S2+S3=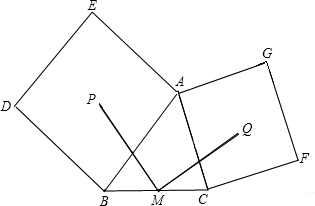
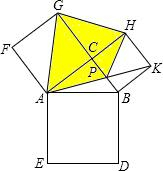如图，正方形ABDE的面积是169平方厘米，正方形CAFG面积是144平方厘米，正方形BCHK的面积是25平方厘米，则阴影四边形AGHP的面积是