题目内容
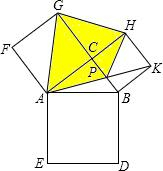 如图,正方形ABDE的面积是169平方厘米,正方形CAFG面积是144平方厘米,正方形BCHK的面积是25平方厘米,则阴影四边形AGHP的面积是
如图,正方形ABDE的面积是169平方厘米,正方形CAFG面积是144平方厘米,正方形BCHK的面积是25平方厘米,则阴影四边形AGHP的面积是分析:根据正方形ABDE的面积、正方形CAFG面积、正方形BCHK的面积可以计算AB,AC,BC,进而判定△ABC为直角三角形,即可求证B、C、G三点共线,且阴影部分的面积为S△AGH+S△APH,故求CP即可解题.
解答:解:根据正方形ABDE的面积、正方形CAFG面积、正方形BCHK的面积
可得AC=12cm,BC=5cm,AB=13cm,且满足AC2+BC2=AB2,
∴△ABC为直角三角形,∴B、C、G三点共线,A、C、H三点共线,
∴
=
=
,
即CP=
cm.
∴阴影部分的面积为S△AGH+S△APH=
AH(GC+CP),
=
×(12+5)(12+
),
=132平方厘米.
故答案为 132.
可得AC=12cm,BC=5cm,AB=13cm,且满足AC2+BC2=AB2,
∴△ABC为直角三角形,∴B、C、G三点共线,A、C、H三点共线,
∴
| CP |
| HK |
| AC |
| AH |
| 12 |
| 17 |
即CP=
| 60 |
| 17 |
∴阴影部分的面积为S△AGH+S△APH=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 60 |
| 17 |
=132平方厘米.
故答案为 132.
点评:本题考查了勾股定理在直角三角形中的运用,勾股定理的逆定理判定直角三角形,正方形各边长相等、各内角为直角的性质,三角形面积的计算,本题中求阴影部分的面积为S△AGH+S△APH=
AH(GC+CP)是解题的关键.
| 1 |
| 2 |

练习册系列答案
相关题目
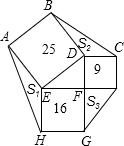 如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,则S1+S2+S3=
如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,则S1+S2+S3=

 如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,则S1+S2+S3=________.
如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,则S1+S2+S3=________.