题目内容
如图,正方形ABDE和ACFG是以△ABC的AB、AC为边的正方形,P、Q为它们的中心,M是BC的中点,试判断MP、MQ在数量和位置是有什么关系?并证明你的结论.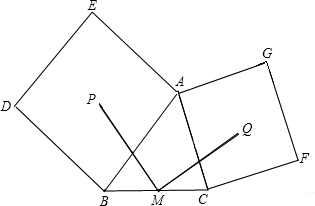
分析:取AB和AC的中点分别为H和K,连接PH、PM、HM、QK、KM、QM,由正方形的性质可知三角形APB与三角形ACQ都为等腰直角三角形,根据直角三角形斜边上的中线等于斜边的一半得到PH等于AB的一半,QK等于AC的一半,然后由MH和MK都为三角形ABC的中位线,根据中位线定理得到HM等于AC的一半,MK等于AB的一半,等量代换得到PH=MK,HM=QK,然后由中位线定理得到MH与AC平行,MK与AB平行,根据两直线平行同位角相等,再等量代换得到∠BHM=∠CKM,两边都加上直角,得到∠PHM=∠MKQ,利用SAS即可得到三角形PMH与三角形KQM全等,根据全等三角形的对应边相等得到PM=QM;由全等得到∠MPH=∠QMK,再由MK与AB平行,得到同位角相等,由PH与AB垂直得到一对锐角互余,等量代换得到∠PMK与∠KMQ互余,即∠PMQ为直角,从而得到PM与QM垂直.
解答:解:MP、MQ之间的关系是MP=MQ,MP⊥MQ,
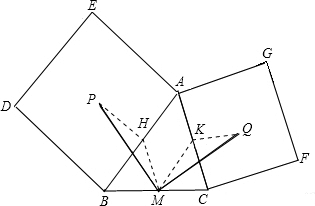
证明:取AB得中点H,AC的中点K,连接PH,HM,PM,QK,KM,MQ,
∵P和Q分别为两正方形的中心,
∴△APB与△AQC都为等腰直角三角形,
∴QK=
AC,PH=
AB(直角三角形斜边上的中线等于斜边的一半),
又HM与KM都为△ABC的中位线,
∴HM=
AC,MK=
AB,
∴QK=HM,MK=PH,
∴HM∥AC,MK∥AB,
∴∠BHM=∠BAC,∠CKM=∠BAC,
∴∠BHM=∠CKM,
又PH⊥AB,QK⊥AC(等腰三角形的三线合一),
∴∠PHB=∠QKC=90°,
∴∠BHM+∠PHB=∠CKM+∠QKC,即∠MHP=∠QKM,
∴△MHP≌△QKM(SAS),
∴PM=QM;
设PM与AB交于点O,
∵△MHP≌△QKM,∴∠HPM=∠KMQ,
∵KM∥AB,∴∠AOP=∠PMO,
∵∠PHB=90°,∴∠HPO+∠POH=90°,
∴∠PMK+∠KMQ=90°,即∠PMQ=90°,
∴PM⊥QM.

证明:取AB得中点H,AC的中点K,连接PH,HM,PM,QK,KM,MQ,
∵P和Q分别为两正方形的中心,
∴△APB与△AQC都为等腰直角三角形,
∴QK=
| 1 |
| 2 |
| 1 |
| 2 |
又HM与KM都为△ABC的中位线,
∴HM=
| 1 |
| 2 |
| 1 |
| 2 |
∴QK=HM,MK=PH,
∴HM∥AC,MK∥AB,
∴∠BHM=∠BAC,∠CKM=∠BAC,
∴∠BHM=∠CKM,
又PH⊥AB,QK⊥AC(等腰三角形的三线合一),
∴∠PHB=∠QKC=90°,
∴∠BHM+∠PHB=∠CKM+∠QKC,即∠MHP=∠QKM,
∴△MHP≌△QKM(SAS),
∴PM=QM;
设PM与AB交于点O,
∵△MHP≌△QKM,∴∠HPM=∠KMQ,
∵KM∥AB,∴∠AOP=∠PMO,
∵∠PHB=90°,∴∠HPO+∠POH=90°,
∴∠PMK+∠KMQ=90°,即∠PMQ=90°,
∴PM⊥QM.
点评:本题主要考查了正方形的性质,矩形的性质和判定,三角形的中位线定理,梯形的中位线定理等知识点,综合运用性质进行证明是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
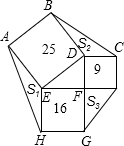 如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,则S1+S2+S3=
如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,则S1+S2+S3=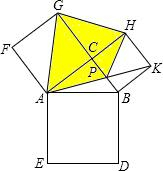 如图,正方形ABDE的面积是169平方厘米,正方形CAFG面积是144平方厘米,正方形BCHK的面积是25平方厘米,则阴影四边形AGHP的面积是
如图,正方形ABDE的面积是169平方厘米,正方形CAFG面积是144平方厘米,正方形BCHK的面积是25平方厘米,则阴影四边形AGHP的面积是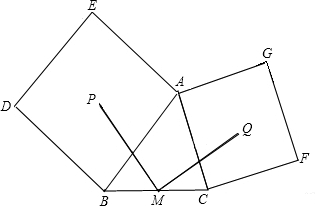
 如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,则S1+S2+S3=________.
如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,则S1+S2+S3=________.