题目内容
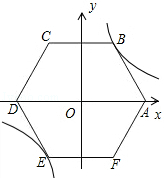
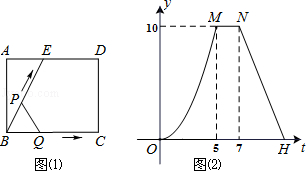
【题目】如图1,放置的一副三角尺,将含45°角的三角尺斜边中点O为旋转中心,逆时针旋转30°得到如图2,连接OB、OD、AD. 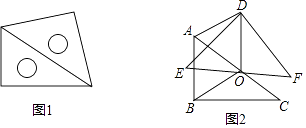
(1)求证:△AOB≌△AOD;
(2)试判定四边形ABOD是什么四边形,并说明理由.
【答案】
(1)证明:根据题意得:∠BAC=60°,∠ABC=∠EDF=90°,EF=AC,
∵O为AC的中点,
∴OB= ![]() AC=OA,OD=
AC=OA,OD= ![]() EF=
EF= ![]() AC=OB,OD⊥EF,
AC=OB,OD⊥EF,
∴△AOB是等边三角形,
∴∠AOB=60°,AB=OB=OA,
由旋转的性质得:∠AOE=30°,
∴∠AOD=90°﹣30°=60°,
在△AOB和△AOD中, 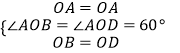 ,
,
∴△AOB≌△AOD(SAS)
(2)解:四边形ABOD是菱形;理由如下:
∵△AOB≌△AOD,
∴AB=AD,
∴AB=AD=OB=OD,
∴四边形ABOD是菱形
【解析】(1)根据题意得:∠BAC=60°,∠ABC=∠EDF=90°,EF=AC,由直角三角形斜边上的中线性质得出OB= ![]() AC=OA,OD=
AC=OA,OD= ![]() EF=
EF= ![]() AC=OB,由等腰三角形的性质得出OD⊥EF,证出△AOB是等边三角形,得出∠AOB=60°,由旋转的性质得:∠AOE=30°,证出∠AOD=60°,由SAS证明△AOB≌△AOD即可;(2)由全等三角形的性质得出AB=AD=OB=OD,即可得出四边形ABOD是菱形.
AC=OB,由等腰三角形的性质得出OD⊥EF,证出△AOB是等边三角形,得出∠AOB=60°,由旋转的性质得:∠AOE=30°,证出∠AOD=60°,由SAS证明△AOB≌△AOD即可;(2)由全等三角形的性质得出AB=AD=OB=OD,即可得出四边形ABOD是菱形.
【考点精析】解答此题的关键在于理解旋转的性质的相关知识,掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

练习册系列答案
相关题目