Question

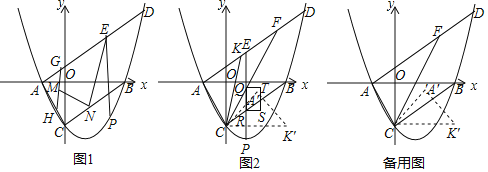
【题目】已知Rt△ABC，∠C=90°，CD⊥AB于D.

(1)点E在CA延长线上，点F在BC延长线上，连接DE，DF，

①如图1，∠B=45°，AC=AE，BC=CF，请补全图形，并直接写出DE和DF的位置关系与数量关系；

②如图2，∠B=30°，若DE和DF的位置关系满足①中的结论，请补全图形，判断AE和CF的数量关系，并证明；

(2)点E在射线CA上，点F在射线BC上，连接DE，DF，BE，EF，如果DE⊥DF，EC=8，EB=17，EF=10，请直接写出AC的长.

Answer 1

【答案】(1)①图形见解析，DE⊥DF，DE=DF；②图形见解析；CF=AE；(2)AC=或.

【解析】

(1)①按照题目要求作图，并写出DE和DF的位置关系与数量关系即可.

②作出图形，根据锐角三角函数 得到又AC=AE，BC=CF，即可得到AE和CF的数量关系.

(2)分两种情况进行讨论.根据勾股定理可得：容易证明根据相似三角形的性质有同理可得通过等量代换得到代入进行计算即可.

(1)①如图所示：

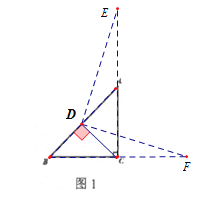
DE⊥DF，DE=DF；

②如图所示：CF=AE；

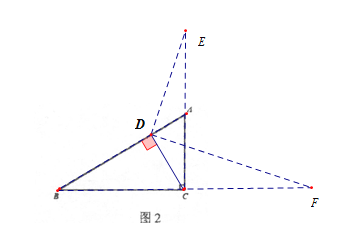
得到

又AC=AE，BC=CF，

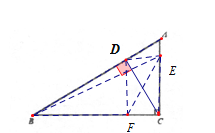
(2)如图：

.根据勾股定理可得：容易证明根据相似三角形的性质有同理可得通过等量代换得到

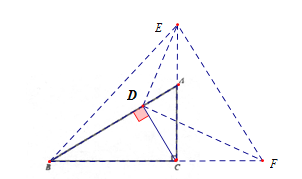
此时，

解得：

解得，