题目内容
如图,在等腰梯形ABCD中,AB∥CD,对角线AC⊥BD于P点,点A在y轴上,点C、D在x轴上.
(1)若BC=10,A(0,8),求点D的坐标;
(2)若BC=13
,AB+CD=34,求过B点的反比例函数的解析式;
(3)如图,在PD上有一点Q,连接CQ,过P作PE⊥CQ交CQ于S,交DC于E,在DC上取EF=DE,过F作FH⊥CQ交CQ于T,交PC于H,当Q在PD上运动时,(不与P、D重合),
的值是否发生变化?若变化,求出变化范围;若不变,求出其值.


(1)若BC=10,A(0,8),求点D的坐标;
(2)若BC=13
| 2 |
(3)如图,在PD上有一点Q,连接CQ,过P作PE⊥CQ交CQ于S,交DC于E,在DC上取EF=DE,过F作FH⊥CQ交CQ于T,交PC于H,当Q在PD上运动时,(不与P、D重合),
| PQ |
| PH |


(1)在等腰梯形ABCD中,AD=BC=10
又∵A(0,8)
∴OA=8
∴OD=
=6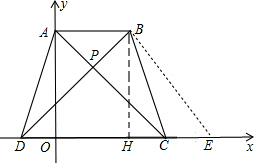
∴D(-6,0)
(2)作BH⊥DE于H,过B点作BE∥AC交x轴于点E,
∵AB∥CE,BE∥AC,
∴ABEC是平行四边形,
∴AB=CE,BE=AC,
又∵ABCD为等腰梯形,
∴AC=BD,
∴BE=BD,
而AC⊥BD,AB∥CE,
∴∠DPC=∠DBE=90°,
∵BH⊥DE,
∴H为DE的中点,即BH为直角三角形DBE斜边DE上的中线,
∴BH=
DE=
(DC+CE)=
(DC+AB)=
×34=17
∵BC=13
∴CH=
=7
∴OH=AB=CE=HE-HC=17-7=10
∴B(10,17)
∴过B点的反比例函数的解析式为:
y=
(3)过点D作DN∥PC交PE的延长线于点M,交HF的延长线于点N,过点M作MI∥EF交BN于点I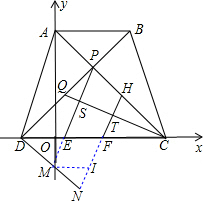
易证四边形EFIM和四边形MNHP是平行四边形
∴MI=EF=DE,MN=PH
又∵∠EDM=∠IMN,∠DEM=∠EFI=∠MIN
∴△EDM≌△IMN
∴DM=MN
∵AC⊥BD,DN∥PC,
∴∠PDM=∠CPQ=90°,∠DPM=∠QCP=90°-∠SPC
由(2)知:∠BDC=45°,而∠DPC=90°,
∴PD=PC
∴△PDM≌△CPQ
∴DM=PQ=PH
∴
=1
又∵A(0,8)
∴OA=8
∴OD=
| 102-82 |

∴D(-6,0)
(2)作BH⊥DE于H,过B点作BE∥AC交x轴于点E,
∵AB∥CE,BE∥AC,
∴ABEC是平行四边形,
∴AB=CE,BE=AC,
又∵ABCD为等腰梯形,
∴AC=BD,
∴BE=BD,
而AC⊥BD,AB∥CE,
∴∠DPC=∠DBE=90°,
∵BH⊥DE,
∴H为DE的中点,即BH为直角三角形DBE斜边DE上的中线,
∴BH=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵BC=13
| 2 |
∴CH=
| BC2-BH2 |
∴OH=AB=CE=HE-HC=17-7=10
∴B(10,17)
∴过B点的反比例函数的解析式为:
y=
| 170 |
| x |
(3)过点D作DN∥PC交PE的延长线于点M,交HF的延长线于点N,过点M作MI∥EF交BN于点I

易证四边形EFIM和四边形MNHP是平行四边形
∴MI=EF=DE,MN=PH
又∵∠EDM=∠IMN,∠DEM=∠EFI=∠MIN
∴△EDM≌△IMN
∴DM=MN
∵AC⊥BD,DN∥PC,
∴∠PDM=∠CPQ=90°,∠DPM=∠QCP=90°-∠SPC
由(2)知:∠BDC=45°,而∠DPC=90°,
∴PD=PC
∴△PDM≌△CPQ
∴DM=PQ=PH
∴
| PQ |
| PH |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目







