题目内容
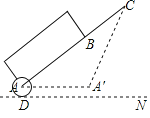
【题目】拉杆箱是人们出行的常用品,采用拉杆箱可以让人们出行更轻松.如图,一直某种拉杆箱箱体长AB=65cm,拉杆最大伸长距离BC=35cm,在箱体底端装有一圆形滚轮,当拉杆拉到最长时,滚轮的圆心在图中的A处,点A到地面的距离AD=3cm,当拉杆全部缩进箱体时,滚轮圆心水平向右平移55cm到A′处,求拉杆把手C离地面的距离(假设C点的位置保持不变).
【答案】拉杆把手C离地面的距离为63cm
【解析】
过C作CE⊥DN于E,延长AA'交CE于F,根据勾股定理即可得到方程652-x2=1002-(55+x)2,求得A'F的长,即可利用勾股定理得到CF的长,进而得出CE的长.
如图所示,过C作CE⊥DN于E,延长AA'交CE于F,则∠AFC=90°,
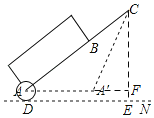
设A'F=x,则AF=55+x,
由题可得,AC=65+35=100,A'C=65,
∵Rt△A'CF中,CF2=652﹣x2,
Rt△ACF中,CF2=1002﹣(55+x)2,
∴652﹣x2=1002﹣(55+x)2,
解得x=25,
∴A'F=25,
∴CF=![]() =60(cm),
=60(cm),
又∵EF=AD=3(cm),
∴CE=60+3=63(cm),
∴拉杆把手C离地面的距离为63cm.

练习册系列答案
相关题目