题目内容
【题目】在△ABC中，AB＝AC，将△ABC沿∠B的平分线折叠，使点A落在BC边上的点D处，设折痕交AC边于点E，继续沿直线DE折叠，若折叠后，BE与线段DC相交，且交点不与点C重合，则∠BAC的度数应满足的条件是_____．
【答案】100°＜∠A＜180°
【解析】
当∠CED＞∠BED时，满足条件，由此构建不等式即可解决问题.
解：如图，
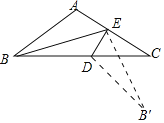
当∠CED＞∠BED时，满足条件，
由翻折可知：∠A＝∠BDE＝∠C+∠DEC，
∴∠DEC＝∠A﹣
（180°﹣∠A）＝
∠A﹣90°，
∵∠AEB＝∠BED＝（180°﹣∠DEC）＝（270°﹣∠A），
∵∠CED＞∠BED，
∴∠A﹣90°＞（270°﹣∠A），
解得∠A＞100°，
∴∠BAC的度数应满足的条件是100°＜∠A＜180°，
故答案为100°＜∠A＜180°．
练习册系列答案
相关题目
