Question

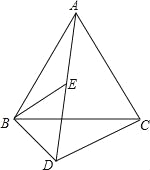
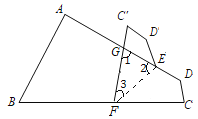
【题目】如图，在四边形 ABCD 中，∠C＋∠D＝210°，E、F 分别是 AD，BC 上的点，将四边形 CDEF 沿直线 EF 翻折，得到四边形 C′D′EF， C′F 交 AD 于点 G，若△EFG 有两个角相等，则∠EFG＝______ °．

Answer 1

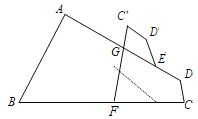
【答案】40 或 50

【解析】

作出辅助线,利用翻折前后的角相等得到∠1+∠GFC=∠1+2∠3=150°,再由三角形的内角和定理得到∠3=∠2-30°,分情况讨论即可解题,见详解.

解：连接EF,如下图,由翻折可知,∠3=∠EFC,

∵∠C＋∠D＝210°,

∴易得∠1+∠GFC=∠1+2∠3=150°,

∵∠1=180°-∠2-∠3,代入式得∠3=∠2-30°,

把代入得∠1+2∠2=210°,

若∠1=∠2,由式可得,∠1=∠2=70°,∠3=40°,

若∠1=∠3,由式可得,∠1=∠3=50°,∠2=80°,

若∠2=∠3,则不成立,说明此种情况不存在,

综上∠EFG=40°或50°.