题目内容
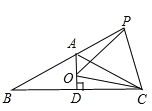
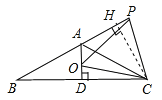
【题目】如图,在等腰三角形ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④![]() .其中所有正确结论的序号为 ( )
.其中所有正确结论的序号为 ( )
A.①②③ B.①②④ C.①③④ D.①②③④
【答案】D.
【解析】
试题解析:连接OB,
∵AB=AC,AD⊥BC,
∴BD=CD,∠BAD=![]() ∠BAC=
∠BAC=![]() ×120°=60°,
×120°=60°,
∴OB=OC,∠ABC=90°-∠BAD=30°,
∵OP=OC,
∴OB=OC=OP,
∴∠APO=∠ABO,∠DCO=∠DBO,
∴∠APO+∠DCO=∠ABO+∠DBO=∠ABD=30°;
故①正确;
∵∠APC+∠DCP+∠PBC=180°,
∴∠APC+∠DCP=150°,
∵∠APO+∠DCO=30°,
∴∠OPC+∠OCP=120°,
∴∠POC=180°-(∠OPC+∠OCP)=60°,
∵OP=OC,
∴△OPC是等边三角形;
故②正确;
在AC上截取AE=PA,
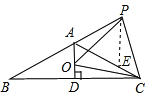
∵∠PAE=180°-∠BAC=60°,
∴△APE是等边三角形,
∴∠PEA=∠APE=60°,PE=PA,
∴∠APO+∠OPE=60°,
∵∠OPE+∠CPE=∠CPO=60°,
∴∠APO=∠CPE,
∵OP=CP,
在△OPA和△CPE中,
∴△OPA≌△CPE(SAS),
∴AO=CE,
∴AC=AE+CE=AO+AP;
故③正确;
过点C作CH⊥AB于H,
∵∠PAC=∠DAC=60°,AD⊥BC,
∴CH=CD,
∴S△ABC=![]() AB
AB![]() CH,
CH,
S四边形AOCP=S△ACP+S△AOC=![]() AP
AP![]() CH+
CH+![]() OA
OA![]() CD=
CD=![]() AP
AP![]() CH+
CH+![]() OA
OA![]() CH=
CH=![]() CH
CH![]() (AP+OA)=
(AP+OA)=![]() CH
CH ![]() AC,
AC,
∴S△ABC=S四边形AOCP;
故④正确.
故选D.