题目内容
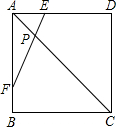正方形ABCD中，E、F分别在边AD，AB上，且AE=BF=| 1 | 3 |
（1）求EF：AE的值；
（2）设AB=x，四边形BCPF的面积为y，求y关于x的函数解析式．
分析：（1）欲求EF：AE的值，由题知EF、AE均与AB相关，可以先求出EF=
AB，AE=BF=
AB，再求值；
（2）AB=x，四边形BCPF的面积为y，欲求y关于x的函数解析式，可以通过图形△APF、△APE、△AEF、△ABC、正方形ABCD相互间的面积进行转换得出．
| ||
| 3 |
| 1 |
| 3 |
（2）AB=x，四边形BCPF的面积为y，欲求y关于x的函数解析式，可以通过图形△APF、△APE、△AEF、△ABC、正方形ABCD相互间的面积进行转换得出．
解答：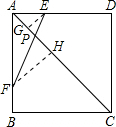
解：（1）∵ABCD是正方形，
∴AB=AD，∠DAB=90°，
∵AE=BF=
AB，
∴AF=
AB，
∴EF=
AB，
∴EF：AE=
：1，
则EF：AE的值为
；
（2）过E、F点作EG⊥AC于G，FH⊥AC于H，
∵S△APF=2S△APE；S△APE+S△APF=S△AEF，
∴S△APF=
S△AEF，
∴S△AEF=AE•AF÷2=
AD×
AB÷2=
x2，
∴S正方形ABCDy=S△ABC-S△AFP=
S正方形ABCD-
S正方形ABCD=
x2．
解：（1）∵ABCD是正方形，∴AB=AD，∠DAB=90°，
∵AE=BF=
| 1 |
| 3 |
∴AF=
| 2 |
| 3 |
∴EF=
| ||
| 3 |
∴EF：AE=
| 5 |
则EF：AE的值为
| 5 |
（2）过E、F点作EG⊥AC于G，FH⊥AC于H，
∵S△APF=2S△APE；S△APE+S△APF=S△AEF，
∴S△APF=
| 2 |
| 3 |
∴S△AEF=AE•AF÷2=
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 9 |
∴S正方形ABCDy=S△ABC-S△AFP=
| 1 |
| 2 |
| 2 |
| 27 |
| 23 |
| 54 |
点评：解答本题要充分利用正方形的特殊性质，考查了相似三角形的性质及勾股定理；运用的是相似三角形的相似比，三角形，正方形的面积计算公式，含线段间的相等关系．
练习册系列答案
阅读快车系列答案
相关题目
（2013•临沂）如图，正方形ABCD中，AB=8cm，对角线AC，BD相交于点O，点E，F分别从B，C两点同时出发，以1cm/s的速度沿BC，CD运动，到点C，D时停止运动，设运动时间为t（s），△OEF的面积为s（cm2），则s（cm2）与t（s）的函数关系可用图象表示为（ ）
如图，在正方形ABCD中，画2个半径为a的四分之一圆，用代数式表示阴影部分的面积为
如图，在正方形ABCD中，AB=4，E在BC边上，BE=1，F是AC上一动点，则EF+BF的最小值是