题目内容
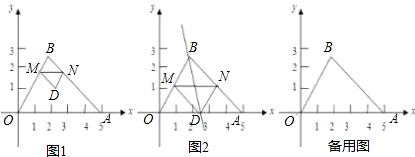
如图①,②,③中,点E,D分别是正△ABC,正四边形ABCM,正五边形ABCMN中以C点为顶点的相邻两边上的点,且BE=CD,DB交AE于P点.(1)图①中,∠APD的度数为60°,图②中,∠APD的度数为90°,图③中,∠APD的度数为
(2)根据前面探索,将本题推广到一般的正n边形情况.如图④,点E,D分别是正n边形ABCM …中以C点为顶点的相邻两边上的点,且BE=CD,BD与AE交于点P,则∠APD的度数为

分析:此题根据正多边形的性质得到各边相等,各角相等,再结合已知条件可以证明△ABE≌△BCD,得到∠BAE=∠CBD.再根据三角形的外角的性质,可以得到∠APD=∠BAE+∠ABP=∠ABP+∠CBD,即∠APD总等于等边三角形一个内角的度数.推而广之,可以得到在正多边形中,∠APD等于对应的正多边形的每一个内角.
解答:解:(1)∵AB=BC,∠ABE=∠BCD,BE=CD,
∴△ABE≌△BCD,
∴∠BAP=∠CBD,
∴∠APD=∠BAE+∠ABP=∠ABP+∠CBD=∠ABE=108°.
(2)同(1)可证,∠APD=正N边形的一个内角=
.
∴△ABE≌△BCD,
∴∠BAP=∠CBD,
∴∠APD=∠BAE+∠ABP=∠ABP+∠CBD=∠ABE=108°.
(2)同(1)可证,∠APD=正N边形的一个内角=
| (n-2)180° |
| n |
点评:此题应当根据正多边形的性质证明一对全等三角形,再结合三角形的外角的性质,发现要求的角总等于正多边形的一个内角.

练习册系列答案
相关题目
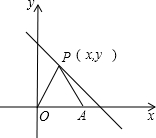 坐标原点,△PAO的面积为S.
坐标原点,△PAO的面积为S.
 15、如图,在平行四边形ABCD中,点E在边BC上,EC=2BE,连接AE交BD于点F,若△BFE的面积为2,则△AFD的面积为
15、如图,在平行四边形ABCD中,点E在边BC上,EC=2BE,连接AE交BD于点F,若△BFE的面积为2,则△AFD的面积为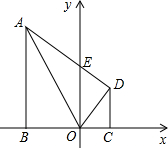 (2011•香坊区模拟)如图,在平面直角坐标系中,点.是坐标原点,AB∥y轴,将△ABO沿A0翻折后,点B落在点D处,AD交y轴于点E,过点D作DC⊥X轴于点C.OB=5,OC=3.
(2011•香坊区模拟)如图,在平面直角坐标系中,点.是坐标原点,AB∥y轴,将△ABO沿A0翻折后,点B落在点D处,AD交y轴于点E,过点D作DC⊥X轴于点C.OB=5,OC=3.