题目内容
知识回顾:(1)如图1,在△ABC中,点D、E、F分别是边AB、BC、AC的中点,我们把△DEF称为△ABC的中点三角形.则S△DEF:S△ABC=
(2)如图2,在正方形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,我们把四边形EFGH称为正方形ABCD的中点四边形,此时四边形EFGH的形状是
(3)实践探究:
如图3,在正五边形ABCDE中,若点F、G、H、M、N分别是边AB、BC、CD、DE、EA的中点,则中点五边形FGHMN的形状是

(4)拓展归纳:
在正n边形A1A2 …An中,若点B1、B2 …Bn分别是边A1A2、A2A3、…、AnA1的中点,则中点n边形B1B2 …Bn的面积与正n边形A1A2 …An的面积之比为Sn边形B1B2…Bn:Sn边形A1A2…An=
分析:(1)利用三角形的中位线定理即可得到两三角形相似且相似比为1:2,故面积为1:4;
(2)易得四边形EFGH为正方形,且面积等于原正方形的面积的一半;
(3)可以利用全等三角形证得五边形为正五边形,设OE交NM于点K,则可得∠ONE=90°,∠OKN=90°,证得△KON∽△NOE,利用面积的比等于相似比的平方,相似比恰恰是∠EON的余弦值,从而得到结论;
(4)按照(3)总结的规律即可得到∠EON为
,从而得到结论.
(2)易得四边形EFGH为正方形,且面积等于原正方形的面积的一半;
(3)可以利用全等三角形证得五边形为正五边形,设OE交NM于点K,则可得∠ONE=90°,∠OKN=90°,证得△KON∽△NOE,利用面积的比等于相似比的平方,相似比恰恰是∠EON的余弦值,从而得到结论;
(4)按照(3)总结的规律即可得到∠EON为
| 180° |
| n |
解答:解:(1)1:4;(1分)
(2)正方形;1:2;(3分)
(3)实践探究:正五边形.(4分)
解:设OE交NM于点K,则可得∠ONE=90°,∠OKN=90°,
又∵∠NOE为公共角,
∴△KON∽△NOE.
设△KON的面积为S1,△NOE的面积为S2,
则
=(
)2.(6分)
∵∠OEN=
∠MEN=
×
=54°,
∴∠EON=36°.
∴
=(
)2=sin254°(或cos236°).
∴S五边形FGHMN:S五边形ABCDE=S1:S2=sin254°(或cos236°)(8分)
(4)拓展归纳:Sn边形B1B2Bn:Sn边形A1A2An=sin2[
]°(或cos2(
)°)(10分)
(2)正方形;1:2;(3分)
(3)实践探究:正五边形.(4分)
解:设OE交NM于点K,则可得∠ONE=90°,∠OKN=90°,
又∵∠NOE为公共角,
∴△KON∽△NOE.
设△KON的面积为S1,△NOE的面积为S2,
则
| S1 |
| S2 |
| ON |
| OE |
∵∠OEN=
| 1 |
| 2 |
| 1 |
| 2 |
| (5-2)×180° |
| 5 |
∴∠EON=36°.
∴
| S1 |
| S2 |
| ON |
| OE |
∴S五边形FGHMN:S五边形ABCDE=S1:S2=sin254°(或cos236°)(8分)
(4)拓展归纳:Sn边形B1B2Bn:Sn边形A1A2An=sin2[
| 90(n-2) |
| n |
| 180 |
| n |
点评:本题考查了相似三角形的判定及性质、等边三角形的性质、三角形的中位线定理等知识,是一道综合性较强的题目,难度较大.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目

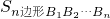 :
: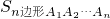 =________.
=________.
 :
: =______.
=______.