题目内容
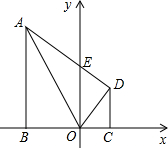 (2011•香坊区模拟)如图,在平面直角坐标系中,点.是坐标原点,AB∥y轴,将△ABO沿A0翻折后,点B落在点D处,AD交y轴于点E,过点D作DC⊥X轴于点C.OB=5,OC=3.
(2011•香坊区模拟)如图,在平面直角坐标系中,点.是坐标原点,AB∥y轴,将△ABO沿A0翻折后,点B落在点D处,AD交y轴于点E,过点D作DC⊥X轴于点C.OB=5,OC=3.(1)求点A的坐标:
(2)点P从A点出发,沿线段A0以
| 5 |
(3)在(2)的条件下,过点Q作射线AD的垂线交射线A0于点N,交x轴于点M,当t为何值时,MN=
| ||
| 4 |
分析:(1)作DH⊥AB于H,由条件和勾股定理可以求出CD=BH=4,BC=DH=8,在Rt△AHD中由勾股定理得AH,从而可以求出AB,进而可以求出A的坐标.
(2)当点Q在线段AD上时,过点P作PF⊥AD于F,当点Q在射线AD上时,过点P作PG⊥AD于G,利用三角形相似就可以用t表示出PF或PG,再利用三角形的面积公式就可以表示出△PDQ的面积.
(3)如图3,如图4,作OK⊥MN,OR⊥MN,利用三角形相似的性质可以用含t的式子表示出PN、MN,再根据MN=
PN.就可以求出其满足条件的t值.
(2)当点Q在线段AD上时,过点P作PF⊥AD于F,当点Q在射线AD上时,过点P作PG⊥AD于G,利用三角形相似就可以用t表示出PF或PG,再利用三角形的面积公式就可以表示出△PDQ的面积.
(3)如图3,如图4,作OK⊥MN,OR⊥MN,利用三角形相似的性质可以用含t的式子表示出PN、MN,再根据MN=
| ||
| 4 |
解答:解:(1)在Rt△ODC中,由勾股定理,得
DC=4.过点D作DH⊥AB于点H,则在Rt△ADH中,
AH2+DH2=AD2
∴(AD-4)2+82=AD2,
∴AD=10,
∴A(-5,10)
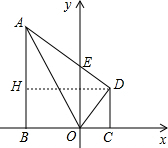
(2)如图1,当点Q在线段AD上时,过点P作PF⊥AD于F.
∴QD=10-3t,AP=
t,由△APF∽△AOD,
∴
=
,
∴PF=t,
∴S△PQD=
QD•PF=-
t2+5t(0<t<
).
当点Q在射线AD上时,过点P作PG⊥AD于G,
∴QD=3t-10,AP=
t,同上得:PG=t,
∴S△PQD=
QD•PG=
t2-5t(
<t≤5).
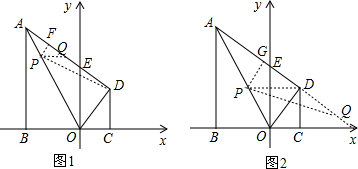
(3)当点Q在线段AQ上时,过点O作OK⊥MN于K,
∴△MOK∽△ODC,
∵OK=QD=10-3t,QN=
t,
∴MK=
(10-3t),MQ=
(10-3t)+5MN=MQ-QN=-
t+
,
∵MN=
PN,
∴MN=
(AN-AP),
∴-
t+
=
(
-
t),
∴t=
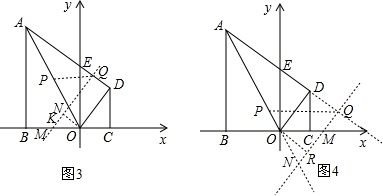
当点Q在射线AD上时,过点O作OR⊥MN于R,
∴△MOR∽△ODC.
∵OR=QD=3t-10,QN=
t.
∴MR=
(3t-10),MQ=5-
(3t-10)=-
t+
,MN=QN-MQ=
t-
,
∵MN=
PN,
∴MN=
(AN-AP),
∴
t-
=
(
-
t),
∴t=4
DC=4.过点D作DH⊥AB于点H,则在Rt△ADH中,
AH2+DH2=AD2
∴(AD-4)2+82=AD2,
∴AD=10,
∴A(-5,10)

(2)如图1,当点Q在线段AD上时,过点P作PF⊥AD于F.
∴QD=10-3t,AP=
| 5 |
∴
| PF |
| 5 |
| ||
5
|
∴PF=t,
∴S△PQD=
| 1 |
| 2 |
| 3 |
| 2 |
| 10 |
| 3 |
当点Q在射线AD上时,过点P作PG⊥AD于G,
∴QD=3t-10,AP=
| 5 |
∴S△PQD=
| 1 |
| 2 |
| 3 |
| 2 |
| 10 |
| 3 |

(3)当点Q在线段AQ上时,过点O作OK⊥MN于K,
∴△MOK∽△ODC,
∵OK=QD=10-3t,QN=
| 3 |
| 2 |
∴MK=
| 3 |
| 4 |
| 3 |
| 4 |
| 25 |
| 4 |
| 25 |
| 2 |
∵MN=
| ||
| 4 |
∴MN=
| ||
| 4 |
∴-
| 25 |
| 4 |
| 25 |
| 2 |
| ||
| 4 |
3
| ||
| 2 |
| 5 |
∴t=
| 20 |
| 7 |
当点Q在射线AD上时,过点O作OR⊥MN于R,
∴△MOR∽△ODC.
∵OR=QD=3t-10,QN=
| 3 |
| 2 |
∴MR=
| 3 |
| 4 |
| 3 |
| 4 |
| 9 |
| 4 |
| 25 |
| 2 |
| 15 |
| 4 |
| 25 |
| 2 |
∵MN=
| ||
| 4 |
∴MN=
| ||
| 4 |
∴
| 15 |
| 4 |
| 25 |
| 2 |
| ||
| 4 |
3
| ||
| 2 |
| 5 |
∴t=4

点评:本题考查了翻折变换,点的坐标,三角形的面积,勾股定理的运用,相似三角形的判定与性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目