题目内容
【题目】如图,在△ABC中,∠AOB=125°,把△ABC剪成三部分,边AB、BCAC放在同一直线上,点O都落在直线MN上,且S△BCO:S△CAO:S△ABO=BC:CA:AB,则∠ACB的度数为( )
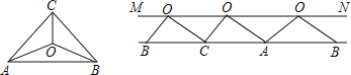
A.70°B.65°C.60°D.85°
【答案】A
【解析】
由S△BCO:S△CAO:S△ABO=BC:CA:AB,得点O为三个内角平分线的交点,根据三角形内角和定理,得∠AOB=90°+![]() ∠ACB,进而即可求解.
∠ACB,进而即可求解.
∵S△BCO:S△CAO:S△ABO=BC:CA:AB,
∴点O到三边的距离相等,
∴点O是△ABC的内心,点O为三个内角平分线的交点,
∴∠AOB+![]() ∠CAB+
∠CAB+![]() ∠ABC=∠ACB+∠CAB+∠ABC=180°,
∠ABC=∠ACB+∠CAB+∠ABC=180°,
∴∠AOB=∠ACB+![]() ∠CAB+
∠CAB+![]() ∠ABC=∠ACB+
∠ABC=∠ACB+![]() (180°-∠ACB),
(180°-∠ACB),
∴∠AOB=90°+![]() ∠ACB,
∠ACB,
∵∠AOB=125°,
∴∠ACB=70°.
故选:A.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目