题目内容
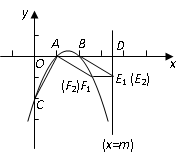
(本题9分)如图9,已知二次函数![]() (
(![]() )的图象经过点
)的图象经过点![]() ,
,![]() ,
,![]() ,直线
,直线![]() (
(![]() )与
)与![]() 轴交于点
轴交于点![]() .
.

1.(1)求二次函数的解析式;
2.(2)在直线![]() (
(![]() )上有一点
)上有一点![]() (点
(点![]() 在第四象限),使得
在第四象限),使得![]() 为顶点的三角形与以
为顶点的三角形与以![]() 为顶点的三角形相似,求
为顶点的三角形相似,求![]() 点坐标(用含
点坐标(用含![]() 的代数式表示);
的代数式表示);
3.(3)在(2)成立的条件下,抛物线上是否存在一点![]() ,使得四边形
,使得四边形![]() 为平行四边形?若存在,请求出F点的坐标;若不存在,请说明理由.
为平行四边形?若存在,请求出F点的坐标;若不存在,请说明理由.
1.(1)根据题意,得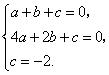
 解得
解得![]() .
.
![]() .
.
2.(2)当△EDB和△AOC相似时,
得![]() 或
或![]() ,
,
∵![]() ,
,
当![]() 时,得
时,得![]() ,
,
∴![]() ,
,
∵点![]() 在第四象限,∴
在第四象限,∴![]() . ……(4分)
. ……(4分)
当![]() 时,得
时,得![]() ,∴
,∴![]() ,
,
∵点![]() 在第四象限,∴
在第四象限,∴![]() .
.
3.(3)假设抛物线上存在一点![]() ,使得四边形
,使得四边形![]() 为平行四边形,则
为平行四边形,则
![]() ,点
,点![]() 的横坐标为
的横坐标为![]() , ……(7分)
, ……(7分)
当点![]() 的坐标为
的坐标为![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ,
,
∵点![]() 在抛物线的图象上,
在抛物线的图象上,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() (舍去),
(舍去),
∴![]() , ……(8分)
, ……(8分)
当点![]() 的坐标为
的坐标为![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ,
,
∵点![]() 在抛物线的图象上,
在抛物线的图象上,
∴![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() (舍去),
(舍去),![]() ,
,
∴![]() ……(9分)
……(9分)
解析:略

练习册系列答案
相关题目




 ,求图中阴影部分的面积.
,求图中阴影部分的面积.