题目内容
(本题10分)
如图,在△ABC中,∠C=90º,BC=5米,AB=10米.M点在线段CA上,从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒.运动时间为t秒.

(1)当t为何值时,△AMN的面积为6米2?
(2)当t为何值时,△AMN的面积最大?并求出这个最大值.
【答案】
(1)t= (2)t=
(2)t=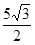 S△AMN=
S△AMN= .
.
【解析】
试题分析:解;(1)三角形的面积等于底乘高除2得到,由题意知;AM=5 -t,AN=2t,过点N做高为x由已知易得∠A=30°∴x=t,∴S△AMN=(5
-t,AN=2t,过点N做高为x由已知易得∠A=30°∴x=t,∴S△AMN=(5 -t)t÷2=6,解得,t=4
-t)t÷2=6,解得,t=4 (不合题意舍去)t=
(不合题意舍去)t= .(2)由(1)得S△AMN=
.(2)由(1)得S△AMN=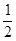 (-t2+5
(-t2+5 t),即-(t-
t),即-(t-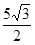 )2+
)2+ .t=
.t=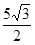 时,S有最大值为
时,S有最大值为

考点:三角形面积公式,直角三角形性质,二次函数最大值的求法。
点评:熟知以上公式性质,解答时,由已知结合公式求得,本题在求三角形的高时,也可利用三角形相似比,求得,做法不唯一。本题有一定的难度,但不大,属于中档题。

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目





 的矩形,它的周长为14,面积为10,求下列各式的值:(1)
的矩形,它的周长为14,面积为10,求下列各式的值:(1) (2)
(2) 

