题目内容
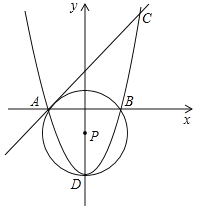
【题目】（14分）在平面直角坐标系中，已知点A（﹣2，0），B（2，0），C（3，5）．
（1）求过点A，C的直线解析式和过点A，B，C的抛物线的解析式；
（2）求过点A，B及抛物线的顶点D的⊙P的圆心P的坐标；
（3）在抛物线上是否存在点Q，使AQ与⊙P相切，若存在请求出Q点坐标．
【答案】（1）y=x+2，
；（2）P（0，
）；（3）Q（
，
）．
【解析】
试题分析：（1）利用抛物线和x轴的两个交点坐标，设出抛物线的解析式
，代入即可得出抛物线的解析式，再设出直线AC的解析式，利用待定系数法即可得出答案；
（2）先求得抛物线的顶点D的坐标，再设点P坐标（0，Py），根据A，B，D三点在⊙P上，得PB=PD，列出关于Py的方程，求解即可得出P点的坐标；
（3）假设抛物线上存在这样的点Q使直线AQ与⊙P相切，设Q点的坐标为（m，m2﹣4），根据平面内两点间的距离公式，即可得出关于m的方程，求出m的值，即可得出点Q的坐标．
试题解析：（1）∵A（﹣2，0），B（2，0）；
∴设二次函数的解析式为y=a（x﹣2）（x+2）…①，把C（3，5）代入①得a=1；
∴二次函数的解析式为：；
设一次函数的解析式为：y=kx+b（k≠0）…②
把A（﹣2，0），C（3，5）代入②得：
，解得：
，∴一次函数的解析式为：y=x+2；
（2）设P点的坐标为（0，
），由（1）知D点的坐标为（0，﹣4）；
∵A，B，D三点在⊙P上，∴PB=PD，∴
，解得： =，∴P点的坐标为（0，）；
（3）在抛物线上存在这样的点Q使直线AQ与⊙P相切．
理由如下：设Q点的坐标为（m，
），根据平面内两点间的距离公式得：
=
，
=
；
∵AP=
，∴
=
；
∵直线AQ是⊙P的切线，∴AP⊥AQ；
∴
，即：=+，解得：
=，
=﹣2（与A点重合，舍去），∴Q点的坐标为（，）．
