题目内容
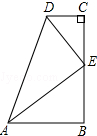
如下图,△ABC中,∠C=90°,∠B=45°,AD是角平分线,DE⊥AB于E,则下列结论不正确的是( )

| A.AC=AE | B.CD=DE | C.CD=DB | D.AB=AC+CD |

B、∵AD是角平分线,DE⊥AB,∠C=90°,
∴CD=DE,故本选项错误;
A、由勾股定理得:AC=
,AE=
,
∴AC=AE,故本选项错误;
D、∵∠B=45°,DE⊥AB,
∴∠BDE=180°-90°-45°=45°=∠B,
∴BE=DE=CD,
∴AB=AE+BE=AC+CD,故本选项错误;
C、∵CD=DE,BD>DE,
∴BD>CD,故本选项正确;
故选C.
∴CD=DE,故本选项错误;
A、由勾股定理得:AC=
| AD2-CD2 |
| AD2-DE2 |
∴AC=AE,故本选项错误;
D、∵∠B=45°,DE⊥AB,
∴∠BDE=180°-90°-45°=45°=∠B,
∴BE=DE=CD,
∴AB=AE+BE=AC+CD,故本选项错误;
C、∵CD=DE,BD>DE,
∴BD>CD,故本选项正确;
故选C.

练习册系列答案
相关题目