题目内容
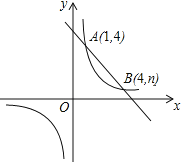
【题目】如图,已知直线y=![]() x与反比例函数y=
x与反比例函数y=![]() (x>0)的图象交于点A(2,m);将直线y=
(x>0)的图象交于点A(2,m);将直线y=![]() x向下平移后与反比例函数y=
x向下平移后与反比例函数y=![]() (x>0)的图象交于点B,且△AOB的面积为3.
(x>0)的图象交于点B,且△AOB的面积为3.
(1)求k的值;
(2)求平移后所得直线的函数表达式.

【答案】(1)k=6;(2)平移后所得直线的函数表达式为y=![]() x﹣3.
x﹣3.
【解析】分析:(1)先根据一次函数解析式求点A的坐标,再利用待定系数法求k的值;
(2)作辅助线AH,得AH=2,根据同底等高的两个三角形面积相等得:S△AOB=S△AOC=3,可得OC=3,写出C(0,-3),根据平行可设直线BC的函数表达式为y=![]() x+b,代入点C的坐标可得解析式.
x+b,代入点C的坐标可得解析式.
详解:(1)∵点A(2,m)在直线y=![]() x上,
x上,
∴m=![]() =3,则A(2,3);
=3,则A(2,3);
又点A(2,3)在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴3=![]() ,则k=6;
,则k=6;
(2)设平移后的直线与y轴交于点C,连接AC,过点A作AH⊥y轴于H,

则AH=2,
∵BC∥OA,
∴S△AOB=S△AOC=3,
∴![]() OCAH=
OCAH=![]() OC2=3,
OC2=3,
则OC=3,
∵点C在y轴的负半轴上,
∴C(0,﹣3),
设直线BC的函数表达式为y=![]() x+b,
x+b,
∴将C(0,﹣3)代入得:b=﹣3,
∴平移后所得直线的函数表达式为y=![]() x﹣3.
x﹣3.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目