Question

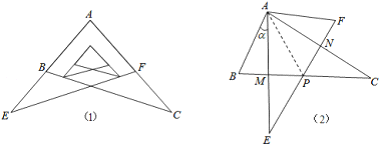
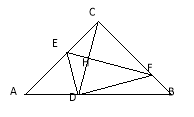
【题目】如图，已知在等腰 Rt△ABC中，∠C＝90°，斜边AB＝2，若将△ABC翻折，折痕EF分别交边AC、边BC于点E和点F（点E不与A点重合，点F不与B点重合），且点C落在AB边上，记作点D．过点D作DK⊥AB，交射线AC于点K，设AD＝x，y＝cot∠CFE，

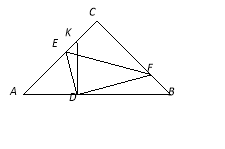
（1）求证：△DEK∽△DFB；

（2）求y关于x的函数解析式并写出定义域；

（3）联结CD，当＝时，求x的值．

Answer 1

【答案】（1）证明见解析（2）y＝,定义域：2－＜x＜ （3）x＝－1或3－．

【解析】

试题分析：（1）利用等腰直角三角形的性质证明∠EKD＝∠B，利用图形折叠的性质得到∠EDK=∠FDB，即可得出结论；（2）利用△DEK∽△DFB，得出＝，从而y＝cot∠CFE＝cot∠DFE＝＝

代入化简即可，定义域：2－＜x＜ （3）取线段EF的中点O，连接OC、OD，根据直角三角形斜边上的中线等于斜边的一半可得OC=OD=EF．设EF与CD交点为H，根据轴对称的性质可得EF⊥CD，且CH=DH=CD．由可得tan∠HOC=，从而得到∠HOC=60°,然后分①若点K在线段AC上和②若点K在线段AC的延长线上，两种情况讨论，得到y的值，再把y的值代入函数解析式就可求出x的值．

试题解析：（1）在等腰 Rt△ABC中，∠C＝90°，∴∠A＝∠B=45°

又∵DK⊥AB,∴∠EKD＝45°∴∠EKD＝∠B

∵将△ABC翻折后点C落在AB边上的点D处

∴∠EDF=∠C＝90°

∵∠KDA= ∠KDB=90°

∴∠EDK=90°－∠KDF, ∠FDB=90°－∠KDF

∴∠EDK=∠FDB

∴△DEK∽△DFB

(说明：点K在线段AC延长线上时等同于在线段上的相似的情况，故不必分类证明)

（2）∵△DEK∽△DFB，∴＝

∵∠DFE＝∠CFE，∴y＝cot∠CFE＝cot∠DFE＝＝

∵AD＝x，AB＝2，∴DK＝AD＝x，DB＝2－x，∴＝，∴y＝

定义域：2－＜x＜

（3）方法一：设CD与EF交于点H，CD被折痕EF垂直平分，CD=2 CH

∵＝，∴=，设CH=，EF=4

∵CD⊥EF,∠C＝90°

∴∠EHC＝∠CHF=90°, ∠ECH=∠CFH=90°－∠HCF

∴△ECH∽△CFH, 得：∴=, 即

设EH=a，则得： 解得：

当EH=k时，∠ECHspan>=∠CFE=30°,

∴y＝＝cot30°＝，∴x＝－1；

当EH=3k时，∠ECH=∠CFE=60°,

∴y＝＝cot60°＝，∴x＝3－；

经检验：x＝－1，x＝3－分别是原各方程的根，且符合题意；

综上所述，x＝－1或x＝3－．

方法二：设CD与EF交于点H，取EF的中点O，联结OC，

∴CH⊥EF，CH＝CD，CO＝EF．

∵＝，∴＝．

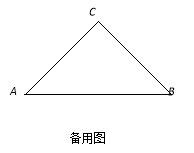
当0＜AD＜1时（如图备一），在Rt△COH中，∠COH＝60°，

∴∠CFE＝30°，∴y＝＝cot30°＝，∴x＝－1；

当1＜AD＜2时（如图备二），

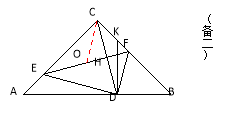
在Rt△COH中，∠COH＝60°，

∴∠CFE＝60°，∴y＝＝cot60°＝，∴x＝3－．

经检验：x＝－1，x＝3－分别是原各方程的根，且符合题意；

综上所述，x＝－1或x＝3－．