题目内容
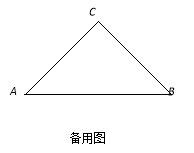
【题目】如图,在△ABC中,BO、CO分别是∠ABC、∠ACB的角平分线,求:

(1)若∠A=50°,求∠BOC的度数.
(2)在其他条件不变的情况下,若∠A=n°,则∠A与∠BOC之间有怎样的数量关系?
【答案】(1)115°;(2)∠BOC=90°+![]() ∠A.
∠A.
【解析】
试题分析:(1)根据三角形的内角和得到∠ABC+∠ACB=180°-∠A=130°,由于BO、CO分别是△ABC的角∠ABC、∠ACB的平分线,得到∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,根据三角形的内角和即可得到结论;
∠ACB,根据三角形的内角和即可得到结论;
(2)根据∠ABC与∠ACB的平分线相交于点O,得到∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,于是得到∠OBC+∠OCB=
∠ACB,于是得到∠OBC+∠OCB=![]() (∠ABC+∠ACB),根据三角形内角和即可得到结论.
(∠ABC+∠ACB),根据三角形内角和即可得到结论.
试题解析:(1)∵∠A=50°,
∴∠ABC+∠ACB=180°-∠A=130°,
∵BO、CO分别是△ABC的角∠ABC、∠ACB的平分线,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∴∠OBC+∠OCB=![]() (∠ABC+∠ACB)=65°,
(∠ABC+∠ACB)=65°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-65°=115°;
(2)∵∠ABC与∠ACB的平分线相交于点O,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∴∠OBC+∠OCB=![]() (∠ABC+∠ACB),
(∠ABC+∠ACB),
在△OBC中,
∠BOC=180°-(∠OBC+∠OCB)
=180°-![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)
=180°-![]() (180°-∠A)
(180°-∠A)
=90°+![]() ∠A,
∠A,
即∠BOC=90°+![]() ∠A.
∠A.
考点: 三角形内角和定理.

练习册系列答案
相关题目