题目内容
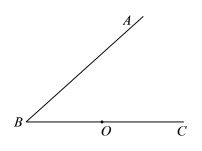
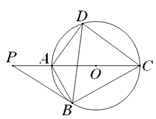
【题目】如图,点P是圆O直径CA延长线上的一点,PB切圆O于点B,点D是圆上的一点,连接AB,AD,BD,CD,∠P=30°.
(1)求证:PB=BC;
(2)若AD=6,tan∠DCA=![]() ,求BD的长.
,求BD的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)如图,连接OB,根据切线的性质易得∠POB=60°,再根据外角的性质求得∠PCB=30°,则PB=PC得证;(2)如图过A点作AM⊥BD,根据圆周角定理得到∠ADB=∠ACB=30°,∠ABD=∠DCA,再根据锐角三角函数求出DM、AM的长,再由tan∠DCA=![]() 求出BM的长,即可求出BD的长.
求出BM的长,即可求出BD的长.
(1)如图所示,连接OB.
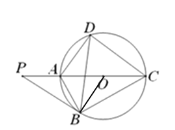
∵PB是切线,∴∠OBP=90°,
∴∠POB=90°-∠P=60°,
∵OB=OC,∴∠OBC=∠OCB,
∴∠PCB=![]() ∠POB=30°,
∠POB=30°,
∴∠P=∠PCB,∴PB=PC.
(2)如图过A点作AM⊥BD,
∠ADB=∠ACB=30°,∠ABD=∠DCA,
∴DM=ADcos30°=3![]() ,AM=ADsin30°=3,
,AM=ADsin30°=3,
∵tan∠ABD=tan∠DCA=![]() ,
,
∴![]() ,
,
∴BM=4,
∴BD=BM+DM=4+3![]() .
.


【题目】北京世界园艺博览会(简称“世园会”)园区4月29日正式开园,门票价格如下:
票种 | 票价(元/人) | |
指定日 | 普通票 | 160 |
优惠票 | 100 | |
平日 | 普通票 | 120 |
优惠票 | 80 | |
注1:“指定日”为开园日(4月29日)、五一劳动节(5月1日)、端午节、中秋节、十一假期(含闭园日),“平日”为世园会会期除“指定日”外的其他日期;
注2:六十周岁及以上老人、十八周岁以下的学生均可购买优惠票;
注3:提前两天及以上在线上购买世园会门票,票价可打九折,但仅限于普通票.
某大家庭计划在6月1日集体入园参观游览,通过计算发现:若提前两天线上购票所需费用为996元,而入园当天购票所需费用为1080元,则该家庭中可以购买优惠票的有______人.