题目内容
如图,在平面直角坐标系中,抛物线 经过点A(
经过点A( ,0)和点B(1,
,0)和点B(1, ),与x轴的另一个交点为C.
),与x轴的另一个交点为C.
(1)求抛物线的函数表达式;
(2)点D在对称轴的右侧,x轴上方的抛物线上,且∠BDA=∠DAC,求点D的坐标;
(3)在(2)的条件下,连接BD,交抛物线对称轴于点E,连接AE.
①判断四边形OAEB的形状,并说明理由;
②点F是OB的中点,点M是直线BD的一个动点,且点M与点B不重合,当∠BMF= ∠MFO时,请直接写出线段BM的长.
∠MFO时,请直接写出线段BM的长.

 经过点A(
经过点A( ,0)和点B(1,
,0)和点B(1, ),与x轴的另一个交点为C.
),与x轴的另一个交点为C.(1)求抛物线的函数表达式;
(2)点D在对称轴的右侧,x轴上方的抛物线上,且∠BDA=∠DAC,求点D的坐标;
(3)在(2)的条件下,连接BD,交抛物线对称轴于点E,连接AE.
①判断四边形OAEB的形状,并说明理由;
②点F是OB的中点,点M是直线BD的一个动点,且点M与点B不重合,当∠BMF=
 ∠MFO时,请直接写出线段BM的长.
∠MFO时,请直接写出线段BM的长.
(1) 。
。
(2)D(4, )。
)。
(3)①四边形OAEB是平行四边形。理由如见解析
②线段BM的长为 或
或 。
。
 。
。(2)D(4,
 )。
)。(3)①四边形OAEB是平行四边形。理由如见解析
②线段BM的长为
 或
或 。
。试题分析:(1)根据点在曲线上点的坐标满足方程的关系,利用待定系数法求出抛物线的函数表达式。
(2)由∠BDA=∠DAC,可知BD∥x轴,点B与点D纵坐标相同,解一元二次方程求出点D的坐标。
(3)①由BE与OA平行且相等,可判定四边形OAEB为平行四边形。
②点M在点B的左右两侧均有可能,需要分类讨论:
∵O(0,0),B(1,
 ),F为OB的中点,∴F(
),F为OB的中点,∴F( ,
, )。
)。过点F作FN⊥直线BD于点N,则FN=
 ﹣
﹣ =
= ,BN=1﹣
,BN=1﹣ =
= 。
。在Rt△BNF中,由勾股定理得:
 。
。∵∠BMF=
 ∠MFO,∠MFO=∠FBM+∠BMF,∴∠FBM=2∠BMF。
∠MFO,∠MFO=∠FBM+∠BMF,∴∠FBM=2∠BMF。(I)当点M位于点B右侧时.
在直线BD上点B左侧取一点G,使BG=BF=
 ,连接FG,则GN=BG﹣BN=1,
,连接FG,则GN=BG﹣BN=1,在Rt△FNG中,由勾股定理得:
 。
。
∵BG=BF,∴∠BGF=∠BFG。
又∵∠FBM=∠BGF+∠BFG=2∠BMF,
∴∠BFG=∠BMF。
又∵∠MGF=∠MGF,∴△GFB∽△GMF。
∴
 ,即
,即 。
。∴BM=
 。
。(II)当点M位于点B左侧时,
设BD与y轴交于点K,连接FK,则FK为Rt△KOB斜边上的中线,
∴KF=
 OB=FB=
OB=FB= 。∴∠FKB=∠FBM=2∠BMF。
。∴∠FKB=∠FBM=2∠BMF。又∵∠FKB=∠BMF+∠MFK,∴∠BMF=∠MFK。∴MK=KF=
 。
。∴BM=MK+BK=
 +1=
+1= 。
。综上所述,线段BM的长为
 或
或 。
。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



 )
)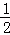 时,y的值.
时,y的值.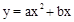 。
。 。
。 中,当x>0时,y随x的增大而增大,则二次函数y=m x2+m x的图象大致是下图中的
中,当x>0时,y随x的增大而增大,则二次函数y=m x2+m x的图象大致是下图中的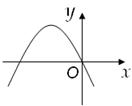


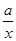 与正比例函数y=(b+c)x在同一坐标系中的大致图像可能是( )
与正比例函数y=(b+c)x在同一坐标系中的大致图像可能是( )