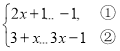题目内容
【题目】根据条件求二次函数的解析式：
（1）抛物线的顶点坐标为（﹣1，﹣1），且与y轴交点的纵坐标为﹣3
（2）抛物线在x轴上截得的线段长为4，且顶点坐标是（3，﹣2）．
【答案】（1）y=﹣2x2﹣4x﹣3；（2）y=
x2﹣3x+
【解析】试题分析：应用待定系数法，求出每个二次函数的解析式各是多少即可．
试题解析：（1）∵抛物线的顶点坐标为（﹣1，﹣1），
∴设抛物线的解析式为：y=a（x+1）2﹣1，
∵抛物线与y轴交点的纵坐标为﹣3，
∴﹣3=a（0+1）2﹣1，
解得a=﹣2．
∴抛物线的解析式是y=﹣2（x+1）2﹣1，
即y=﹣2x2﹣4x﹣3
（2）∵抛物线的顶点坐标是（3，﹣2），
∴抛物线的对称轴为直线x=3，
∵抛物线在x轴上截得的线段长为4，
∴抛物线与x轴的两交点坐标为（1，0），（5，0），
设抛物线的解析式为y=k（x﹣1）（x﹣5），
则﹣2=k（3﹣1）（3﹣5）
解得k= 
，
∴抛物线解析式为y=
（x﹣1）（x﹣5），
即y=
x2﹣3x+
练习册系列答案
一本好题口算题卡系列答案
相关题目
