Question

【题目】（阅读理解）

在解方程组或求代数式的值时，可以用整体代入或整体求值的方法，化难为易．

（1）解方程组

（2）已知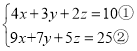，求x+y+z的值

解：（1）把②代入①得：x+2×1＝3．解得：x＝1．

把x＝1代入②得：y＝0．

所以方程组的解为，

（2）①×2得：8x+6y+4z＝20．③

②﹣③得：x+y+z＝5．

（类比迁移）

（1）若，则x+2y+3z＝　 　．

（2）解方程组

（实际应用）

打折前，买39件A商品，21件B商品用了1080元．打折后，买52件A商品，28件B商品用了1152元，比不打折少花了多少钱？

Answer 1

【答案】【类比迁移】（1）18；（2）；【实际应用】比不打折少花了288元．

【解析】

（1）中的两式相加再除以2即可得出答案；

（2）先对①移项得到2x﹣y＝2，再将2x﹣y＝2带入②，即可求出答案；

【实际应用】

设打折前A商品每件x元，B商品每件y元，由题意得：39x+21y＝1080，即可求出答案.

（1），

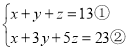（①+②）÷2，得：x+2y+3z＝18．

故答案为：18．

（2），

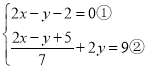由①得：2x﹣y＝2③，

将③代入②中得：1+2y＝9，解得：y＝4，

将y＝4代入①中得：x＝3．

∴方程组的解为．

（实际应用）

设打折前A商品每件x元，B商品每件y元，

根据题意得：39x+21y＝1080，

即13x+7y＝360，

将两边都乘4得：52x+28y＝1440，

1440﹣1152＝288（元）．

答：比不打折少花了288元．