题目内容
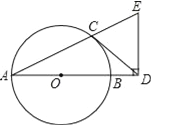
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
(1)求证:DC=DE;
(2)若tan∠CAB=![]() ,AB=3,求BD的长.
,AB=3,求BD的长.
【答案】(1)证明见解析;(2)1.
【解析】
试题分析:(1)利用切线的性质结合等腰三角形的性质得出∠DCE=∠E,进而得出答案;
(2)设BD=x,则AD=AB+BD=3+x,OD=OB+BD=1.5+x,利用勾股定理得出BD的长.
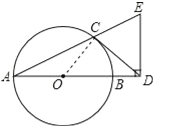
试题解析:(1)证明:连接OC,∵CD是⊙O的切线,∴∠OCD=90°,∴∠ACO+∠DCE=90°,又∵ED⊥AD,∴∠EDA=90°,∴∠EAD+∠E=90°,∵OC=OA,∴∠ACO=∠EAD,故∠DCE=∠E,∴DC=DE,(2)解:设BD=x,则AD=AB+BD=3+x,OD=OB+BD=1.5+x,在Rt△EAD中,∵tan∠CAB=![]() ,∴ED=
,∴ED=![]() AD=
AD=![]() (3+x),由(1)知,DC=
(3+x),由(1)知,DC=![]() (3+x),在Rt△OCD中,
(3+x),在Rt△OCD中,![]() ,则
,则![]() ,解得:
,解得:![]() =﹣3(舍去),
=﹣3(舍去),![]() =1,故BD=1.
=1,故BD=1.

练习册系列答案
相关题目