Question

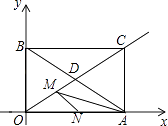
【题目】如图，在矩形ABCD中，对角线AC、BD相交于点O，点E、F分别是AO、AD的中点，若AB＝6 cm，BC＝8 cm，则△AEF的周长为________cm．

Answer 1

【答案】9

【解析】利用勾股定理求出AC，再根据矩形的对角线互相平分且相等求出OA=OD=AC，然后根据三角形的中位线平行于第三边并且等于第三边的一半可得EF=OD，再求出AF，AE，然后根据三角形的周长公式列式计算即可得解．

解：由勾股定理得，AC===10cm，

∵四边形ABCD是矩形，

∴OA=OD=AC=×10=5cm，

∵点E、F分别是AO、AD的中点，

∴EF=OD=cm，

AF=×8=4cm，

AE=OA=cm，

∴△AEF的周长=+4+=9cm.

故答案为：9.