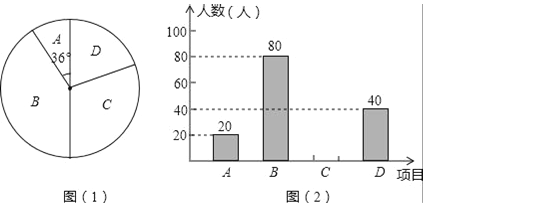
题目内容
【题目】若顺次连接四边形ABCD各边中点所得四边形是矩形,则四边形ABCD必然是( )
A.菱形
B.对角线相互垂直的四边形
C.正方形
D.对角线相等的四边形
【答案】B
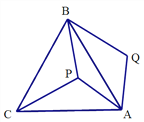
【解析】解:已知:如图,四边形EFGH是矩形,且E、F、G、H分别是AB、BC、CD、AD的中点, 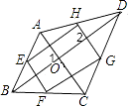
求证:四边形ABCD是对角线垂直的四边形.
证明:由于E、F、G、H分别是AB、BC、CD、AD的中点,
根据三角形中位线定理得:EH∥FG∥BD,EF∥AC∥HG;
∵四边形EFGH是矩形,即EF⊥FG,
∴AC⊥BD;故答案为:B.
题目中并没有给出图,画图证明进行对题意的分析。
如图所示,四边形EFGH是矩形,矩形的性质1矩形的四个角都是直角,所以EF⊥FG,再根据中位线的定义和定理:连接三角形两边中点的线段叫做三角形的中位线(定义),三角形的中位线平行第三边(性质),得结论EF∥AC∥HG,结合EF⊥FG,根据两直线平行,第三条直线垂直于其中一条平行线,那么第三条直线垂直于这两条平行线,所以AC⊥FG,同理EH∥FG∥BD,所以AC⊥BD。

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目