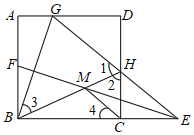
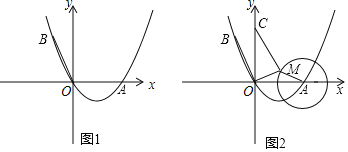题目内容
【题目】在△ABC与△CDE中,∠ACB![]() ∠CDE
∠CDE![]() 90°,AC
90°,AC![]() BC,CD
BC,CD![]() ED,连接AE,BE,F为AE的中点,连接DF,△CDE绕着点C旋转.
ED,连接AE,BE,F为AE的中点,连接DF,△CDE绕着点C旋转.
(1)如图1,当点D落在AC上时,DF与BE的数量关系是: ;
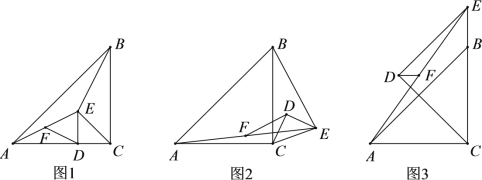
(2)如图2,当△CDE旋转到该位置时,DF与BE是否仍具有(1)中的数量关系,如果具有,请给予证明;如果没有,请说明理由;
(3)如图3,当点E落在线段CB延长线上时,若CD![]() AC
AC![]() 2,求DF的长.
2,求DF的长.
【答案】(1)DF=![]() BE;(2)见解析;(3)
BE;(2)见解析;(3)![]() ;
;
【解析】
(1)证明△ACE≌△BCE,则AE=BE,DF是直角△ADE的中线,DF=![]() AE,即可证明DF=
AE,即可证明DF=![]() BE;
BE;
(2)连接AM,证明△ACM≌△BCE,则AM=BE,DF为△AME的中位线,DF=![]() =
=![]() BE;
BE;
(3)易知CD=DE=2,由勾股定理CE=![]() ,BE=CE—CB=
,BE=CE—CB=![]() ,DF=
,DF=![]() BE,可求得DF=
BE,可求得DF=![]() .
.
(1) ∵∠ACB=∠CDE=90°,AC=BC,CD =ED,
∴∠ACE=∠BCE=45°,
∴△ACE≌△BCE,
∴AE=BE,因为DF是直角△ADE的中线,
∴DF=![]() AE
AE
∴DF=![]() BE
BE
(2)如图,将△CDE沿着CD翻折,得到△DCM≌△DCE,连接AM,

由△CDE为等腰直角三角形易知△CME为等腰直角三角形,
在△ACM和△BCE中,
AC=BC,∠ACM=∠BCE ,CM=CE,
∴△ACM≌△BCE,
∴AM=BE
∵F为AE的中点,D为ME的中点
∴DF为△AME的中位线,
∴DF=![]() ,
,
∴DF=![]() BE.
BE.
(3)将△EDC沿DC翻折得到△DCM
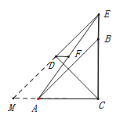
CD=DE=2,由勾股定理可知CE=![]()
BE=CE—CB=![]()
由前面的结论可知:DF=![]() BE
BE
∴DF=![]() .
.

练习册系列答案
相关题目