题目内容
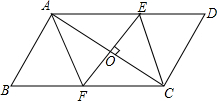如图在平行四边形ABCD中，AC为对角线，EF⊥AC，垂足是O，交AD于E，交BC于F，连接AF、CE．请你探求当点O满足什么条件，四边形AFCE是菱形，说明理由．
答：当O是AC的中点时，四边形AFCE是菱形；
证明：四边形AFCE是菱形，理由是：
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴
=
，
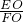∵O是AC的中点，
∴AO=OC，
∴OE=OF，
∴四边形AFCE是平行四边形，
∵EF⊥AC，
∴平行四边形AFCE是菱形
分析：当O是AC的中点时，四边形AFCE是菱形；根据平行四边形性质推出AD∥BC，根据平行线分线段成比例定理求出OE=OF，推出平行四边形AFCE，根据菱形的判定推出即可．
点评：本题考查了平行线分线段成比例定理，平行四边形的性质，菱形的判定等知识点的运用，关键是根据题意推出OE=OF，题目比较典型．
证明：四边形AFCE是菱形，理由是：
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴
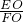=，∵O是AC的中点，
∴AO=OC，
∴OE=OF，
∴四边形AFCE是平行四边形，
∵EF⊥AC，
∴平行四边形AFCE是菱形
分析：当O是AC的中点时，四边形AFCE是菱形；根据平行四边形性质推出AD∥BC，根据平行线分线段成比例定理求出OE=OF，推出平行四边形AFCE，根据菱形的判定推出即可．
点评：本题考查了平行线分线段成比例定理，平行四边形的性质，菱形的判定等知识点的运用，关键是根据题意推出OE=OF，题目比较典型．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
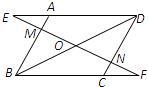21、已知：如图在平行四边形ABCD中，过对角线BD的中点O作直线EF分别交DA的延长线、AB、DC、BC的延长线于点E、M、N、F．
7、如图在平行四边形ABCD中，如果AB=5，AD=9，∠ABC的平分线交AD于点E，交CD的延长线于点F，则DF=
已知如图在平行四边形ABCD中，E、F分别为边AB、CD的中点，BD是对角线．
如图在平行四边形ABCD中，AD=4cm，AB=2cm，则平行四边形ABCD的周长等于（ ）