Question

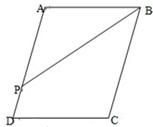
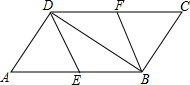已知如图在平行四边形ABCD中，E、F分别为边AB、CD的中点，BD是对角线．
求证：△ADE≌△CBF．

Answer 1

分析：由四边形ABCD是平行四边形，即可得AD=BC，AB=CD，∠A=∠C，又由E、F分别为边AB、CD的中点，可证得AE=CF，然后由SAS，即可判定△ADE≌△CBF．

解答：证明：∵四边形ABCD是平行四边形，
∴AD=BC，AB=CD，∠A=∠C，
∵E、F分别为边AB、CD的中点，
∴AE=

1

2

AB，CF=

1

2

CD，
∴AE=CF，
在△ADE和△CBF中，
∵

AD=BC ∠A=∠C AE=CF

，
∴△ADE≌△CBF（SAS）．

点评：此题考查了平行四边形的性质以及全等三角形的判定．此题难度不大，注意掌握数形结合思想的应用．