题目内容
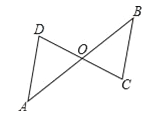
【题目】如图,点O是线段AB和线段CD的中点.
(1)求证:△AOD≌△BOC;
(2)求证:AD∥BC.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)由点O是线段AB和线段CD的中点可得出AO=BO,CO=DO,结合对顶角相等,即可利用全等三角形的判定定理(SAS)证出△AOD≌△BOC;
(2)结合全等三角形的性质可得出∠A=∠B,依据“内错角相等,两直线平行”即可证出结论.
试题解析:(1)∵点O是线段AB和线段CD的中点,∴AO=BO,CO=DO.
在△AOD和△BOC中,∵AO=BO,∠AOD=∠BOC,CO=DO ,∴△AOD≌△BOC(SAS).
(2)∵△AOD≌△BOC,∴∠A=∠B,∴AD∥BC.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
【题目】潼南绿色无公害蔬菜基地有甲、乙两种植户,他们种植了A、B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
种植户 | 种植A类蔬菜面积 | 种植B类蔬菜面积 | 总收入 |
甲 | 3 | 1 | 12500 |
乙 | 2 | 3 | 16500 |
说明:不同种植户种植的同类蔬菜每亩平均收入相等.
(1)求A、B两类蔬菜每亩平均收入各是多少元?
(2)某种植户准备租20亩地用来种植A、B两类蔬菜,为了使总收入不低于63000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案.