题目内容
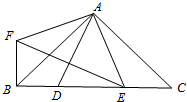 如图,在Rt△ABC中,AB=AC,∠BAC=90°,D、E为BC上两点,∠DAE=45°,F为△ABC外一点,且FB⊥BC,FA⊥AE,则下列结论:①CE=BF;②BD2+CE2=DE2;③
如图,在Rt△ABC中,AB=AC,∠BAC=90°,D、E为BC上两点,∠DAE=45°,F为△ABC外一点,且FB⊥BC,FA⊥AE,则下列结论:①CE=BF;②BD2+CE2=DE2;③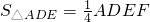 ;④CE2+BE2=2AE2,其中正确的是
;④CE2+BE2=2AE2,其中正确的是
- A.①②③④
- B.①②④
- C.①③④
- D.②③
A
分析:根据等腰直角三角形的性质,判断出△AFB≌△AEC,即可得出CE=BF,根据勾股定理与等量代换可得②正确,根据在等腰三角形中,角平分线与中线为一条直线即可得出③,再根据勾股定理以及等量代换即可得出④.
解答: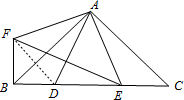 解:①∵∠BAC=90°,FA⊥AE,∠DAE=45°,
解:①∵∠BAC=90°,FA⊥AE,∠DAE=45°,
∴∠CAE=90°-∠DAE-∠BAD=45°-∠BAD,
∠FAB=90°-∠DAE-∠BAD=45°-∠BAD,
∴∠FAB=∠EAC,
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵FB⊥BC,
∴∠FAB=45°,
∴△AFB≌△AEC,
∴CE=BF,故①正确,
②:由①中证明△AFB≌△AEC,
∴AF=AE,
∵∠DAE=45°,FA⊥AE,
∴∠FAD=∠DAE=45°,
∴△AFD≌△AED,
连接FD,
∵FB=CE,
∴FB2+BD2=FD2=DE2,故②正确,
③:∵∠FAD=∠EAD=45°,AF=AE,
∴AD⊥EF,EF=2EG,
∴S△ADE= •AD•EG=
•AD•EG=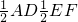 =
= ,
,
故③正确,
④:∵FB2+BE2=EF2,CE=BF,
∴CE2+BE2=EF2,
在RT△AEF中,AF=AE,
AF2+AE2=EF2,
∴EF2=2AE2,
∴CE2+BE2=2AE2,故④正确.
故选A.
点评:本题考查了勾股定理、全等三角形的判定定理以及等腰直角直角三角形的性质,此题涉及的知识面比较广,解题时要注意仔细分析,难度较大.
分析:根据等腰直角三角形的性质,判断出△AFB≌△AEC,即可得出CE=BF,根据勾股定理与等量代换可得②正确,根据在等腰三角形中,角平分线与中线为一条直线即可得出③,再根据勾股定理以及等量代换即可得出④.
解答:
 解:①∵∠BAC=90°,FA⊥AE,∠DAE=45°,
解:①∵∠BAC=90°,FA⊥AE,∠DAE=45°,∴∠CAE=90°-∠DAE-∠BAD=45°-∠BAD,
∠FAB=90°-∠DAE-∠BAD=45°-∠BAD,
∴∠FAB=∠EAC,
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵FB⊥BC,
∴∠FAB=45°,
∴△AFB≌△AEC,
∴CE=BF,故①正确,
②:由①中证明△AFB≌△AEC,
∴AF=AE,
∵∠DAE=45°,FA⊥AE,
∴∠FAD=∠DAE=45°,
∴△AFD≌△AED,
连接FD,
∵FB=CE,
∴FB2+BD2=FD2=DE2,故②正确,
③:∵∠FAD=∠EAD=45°,AF=AE,
∴AD⊥EF,EF=2EG,
∴S△ADE=
 •AD•EG=
•AD•EG=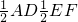 =
= ,
,故③正确,
④:∵FB2+BE2=EF2,CE=BF,
∴CE2+BE2=EF2,
在RT△AEF中,AF=AE,
AF2+AE2=EF2,
∴EF2=2AE2,
∴CE2+BE2=2AE2,故④正确.
故选A.
点评:本题考查了勾股定理、全等三角形的判定定理以及等腰直角直角三角形的性质,此题涉及的知识面比较广,解题时要注意仔细分析,难度较大.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 (2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.
(2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.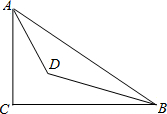 如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD和BD分别是∠BAC和∠ABC的平分线,它们相交于点D,求点D到BC的距离.
如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD和BD分别是∠BAC和∠ABC的平分线,它们相交于点D,求点D到BC的距离.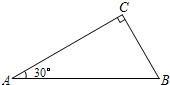 边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直.
边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直.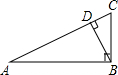 如图,在Rt△ABC中,BD⊥AC,sinA=
如图,在Rt△ABC中,BD⊥AC,sinA= 点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).
点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).