题目内容
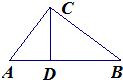 15、如图,CD是Rt△ABC的斜边AB上的高,图中与△ADC相似的三角形为
15、如图,CD是Rt△ABC的斜边AB上的高,图中与△ADC相似的三角形为△ABC
(填一个即可).分析:根据三角形内角和定理可求得∠ACD=∠B,再根据∠A=∠A即可证明△ADC∽△ACB,即可解题.
解答:解:∵∠ACD+∠BCD=90°∠BCD+∠B=90°,
∴∠ACD=∠B,
∵∠A=∠A,
∴△ADC∽△ACB(AA),
故答案可以为:△ABC.
∴∠ACD=∠B,
∵∠A=∠A,
∴△ADC∽△ACB(AA),
故答案可以为:△ABC.
点评:本题考查了三角形内角和定理,相似三角形的证明,本题中求证△ADC∽△ACB是解题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
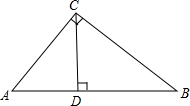 如图,CD是Rt△ABC斜边上的高.若AB=5,AC=3,则tan∠BCD为( )
如图,CD是Rt△ABC斜边上的高.若AB=5,AC=3,则tan∠BCD为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 5、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于( )
5、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于( ) 18、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于
18、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于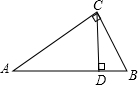 如图,CD是Rt△ABC斜边上的高线,若sinA=
如图,CD是Rt△ABC斜边上的高线,若sinA=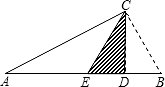 如图,CD是Rt△ABC斜边AB上的高,直角边AC=
如图,CD是Rt△ABC斜边AB上的高,直角边AC=