Question

（1998•河北）已知：如图弦AB经过⊙O的半径OC的中点P，且AP=2，PB=3，则是⊙O的半径等于（　　）

• A．

  2

• B．

  6

• C．2

  2

• D．2

  6

Answer 1

分析：延长CO交⊙O于D，设⊙O的半径是R，则CP=

1

2

R=OP，PD=

1

2

R+R，由相交弦定理得出AP×BP=CP×DP，求出即可．

解答：解：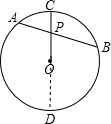
延长CO交⊙O于D，
设⊙O的半径是R，
∵弦AB经过⊙O的半径OC的中点P，
∴CP=

1

2

R=OP，PD=

1

2

R+R，
由相交弦定理得：AP×BP=CP×DP，
则2×3=

1

2

R×（

1

2

R+R），
解得：R=2

2

，
故选C．

点评：本题考查了相交弦定理和解一元二次方程，关键是能根据定理得出关于R的方程．