题目内容
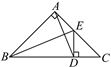
【题目】如图,△ABC是等腰直角三角形,∠BAC=90°,BE是△ABC的角平分线,ED⊥BC于点D,连接AD.
(1)请你写出图中所有的等腰三角形;
(2)若BC=10,求AB+AE的长.
【答案】(1)见解析;(2) AB+AE=10.
【解析】
(1)如图,根据△ABC是等腰直角三角形可知∠8=45°,由ED⊥BC可知∠7=∠8=45°,由此得到△DCE为等腰三角形;由角平分线的性质可知AE=DE,由此得到△AED为等腰三角形;同理可得△ABD为等腰三角形;
(2)由于△AED为等腰三角形,△ABD为等腰三角形,利用等腰三角形的性质即可证明AB+AE=BD+CD=BC,然后就可以求出AB+AE的长.
(1)如图,∵△ABC是等腰直角三角形,∠BAC=90°,
∴∠ABC=∠C=45°.
又∵ED⊥BC,
∴∠EDC=90°,
∴∠7=∠C=45°,
∴DE=DC,

故△DCE为等腰直角三角形.
∵BE是△ABC的角平分线,∠BAC=∠BDE=90°,
∴AE=DE,
∴△ADE为等腰三角形.
∵BE是△ABC的角平分线,
∴∠1=∠2.
又∵∠BAE=∠BDE=90°,BE=BE,
∴△ABE≌△DBE,
∴AB=DB,
∴△ABD为等腰三角形.
故图中所有的等腰三角形为△ABC,△DCE,△ADE,△ABD,共4个.
(2)由(1)可知△ADE为等腰三角形,△ABD为等腰三角形,△DCE为等腰三角形,故AB=DB,AE=DE=DC,∴AB+AE=DB+DC=BC=10.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目