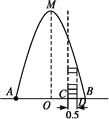
题目内容
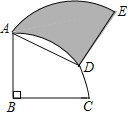
【题目】如图,O为Rt△ABC的直角边AC上一点,以OC为半径的⊙O与斜边AB相切于点D,交OA于点E.已知BC=![]() ,AC=3.
,AC=3.
(1)求AD的长;
(2)求图中阴影部分的面积.

【答案】(1)![]() (2)
(2)![]()
【解析】
(1)首先利用勾股定理求出![]() 的长,再证明
的长,再证明![]() ,进而由
,进而由![]() 可求出;
可求出;
(2)利用特殊角的锐角三角函数可求出![]() 的度数,则圆心角
的度数,则圆心角![]() 的度数可求出,在直角三角形
的度数可求出,在直角三角形![]() 中求出
中求出![]() 的长,最后利用扇形的面积公式即可求出阴影部分的面积.
的长,最后利用扇形的面积公式即可求出阴影部分的面积.
(1)在Rt△ABC中,∵![]() ,AC=3,
,AC=3,
∴![]() ,
,
∵BC⊥OC,
∴BC是圆的切线,
∵⊙O与斜边AB相切于点D,
∴BD=BC,
∴![]() ;
;
(2)在Rt△ABC中,
∵![]() ,
,
∴∠A=30°,
∵⊙O与斜边AB相切于点D,
∴OD⊥AB,
∴∠AOD=90°-∠A=60°,
∵![]() ,
,
∴![]() ,
,
∴OD=1,
∴![]() .
.

练习册系列答案
相关题目