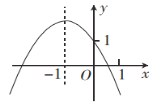题目内容
【题目】如图,抛物线与x轴交于A、B两点,与y轴交C点,点A的坐标为(2,0),点C的坐标为(0,3)它的对称轴是直线![]()
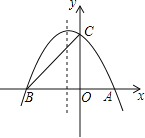
(1)求抛物线的解析式;
(2)M是线段AB上的任意一点,当△MBC为等腰三角形时,求M点的坐标.
【答案】(1)![]()
(2)M点坐标为(0,0)或![]()
【解析】
(1)根据抛物线的对称轴得到抛物线的顶点式,然后代入已知的两点理由待定系数法求解即可。
(2)首先求得点B的坐标,然后分CM=BM时和BC=BM时两种情况根据等腰三角形的性质求得点M的坐标即可。
解:(1)∵抛物线的对称轴是直线![]() ,∴设抛物线的解析式
,∴设抛物线的解析式![]() 。
。
把A(2,0)C(0,3)代入得: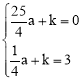 ,解得:
,解得: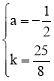 。
。
∴抛物线的解析式为![]() ,即
,即![]() 。
。
(2)由y=0得![]() ,∴x1=1,x2=﹣3。
,∴x1=1,x2=﹣3。
∴B(﹣3,0)。
分两种情况讨论(因为BC=MC时,点M已不在线段AB上,无需考虑):
①CM=BM时,
∵BO=CO=3, 即△BOC是等腰直角三角形,
∴当M点在原点O时,△MBC是等腰三角形。
∴M点坐标(0,0)。
②BC=BM时,
在Rt△BOC中,BO=CO=3,∴由勾股定理得![]() 。
。
∴BM=![]() 。
。
∴M点坐标![]() 。
。
综上所述,当△MBC为等腰三角形时,M点坐标为(0,0)或![]() 。
。
题型】解答题

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目