题目内容
(2013年四川攀枝花6分)如图,直线y=k1x+b(k1≠0)与双曲线 (k2≠0)相交于A(1,2)、B(m,﹣1)两点.
(k2≠0)相交于A(1,2)、B(m,﹣1)两点.
(1)求直线和双曲线的解析式;
(2)若A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且x1<0<x2<x3,请直接写出y1,y2,y3的大小关系式;
(3)观察图象,请直接写出不等式k1x+b< 的解集.
的解集.
解:(1)将A(1,2)代入双曲线解析式得:k2=2,即双曲线解析式为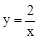 。
。
将B(m,﹣1)代入双曲线解析式得: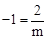 ,即m=﹣2,∴B(﹣2,﹣1)。
,即m=﹣2,∴B(﹣2,﹣1)。
将A与B坐标代入直线解析式得: ,解得:
,解得: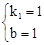 。
。
∴直线解析式为y=x+1。
(2)y2>y3>y1。
(3)由A(1,2),B(﹣2,﹣1),
利用函数图象得:不等式k1x+b< 的解集为﹣2<x<0或x>1。
的解集为﹣2<x<0或x>1。
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
我市某商场有甲、乙两种商品,甲种每件进价15元,售价20元;乙种每件进价35元,售价45元.
(1)若商家同时购进甲、乙两种商品100件,设甲商品购进x件,售完此两种商品总利润为y 元.写出y与x的函数关系式.
(2)该商家计划最多投入3000元用于购进此两种商品共100件,则至少要购进多少件甲种商品?若售完这些商品,商家可获得的最大利润是多少元?
(3)“五•一”期间,商家对甲、乙两种商品进行表中的优惠活动,小王到该商场一次性付款324元购买此类商品,商家可获得的最小利润和最大利润各是多少?
| 打折前一次性购物总金额 | 优惠措施 |
| 不超过400元 | 售价打九折 |
| 超过400元 | 售价打八折 |
已知点A( ,
, )在抛物线
)在抛物线 上,则点A关于抛物线对称轴的对称点坐标为
上,则点A关于抛物线对称轴的对称点坐标为
| A.(-3,7) | B.(-1,7) | C.(-4,10) | D.(0,10) |
 ,求:
,求: 轴,
轴, 轴的交点坐标;
轴的交点坐标; 的图象与一次函数
的图象与一次函数 的图象交于点A(1,4)和点B
的图象交于点A(1,4)和点B ,
, ).
).
 >0时,直接写出
>0时,直接写出 >
> 时自变量
时自变量
