题目内容
【题目】已知△ABC中,a、b、c分别为∠A、∠B、∠C的对边,方程![]() 是关于x的一元二次方程.
是关于x的一元二次方程.
(1)判断方程![]() 的根的情况为 (填序号);
的根的情况为 (填序号);
①方程有两个相等的实数根; ②方程有两个不相等的实数根;
③方程无实数根; ④无法判断
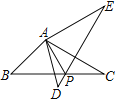
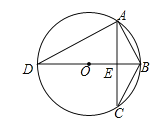
(2)如图,若△ABC内接于半径为2的⊙O,直径BD⊥AC于点E,且∠DAC=60°,求方程![]() 的根;
的根;
(3)若![]() 是方程
是方程![]() 的一个根,△ABC的三边a、b、c的长均为整数,试求a、b、c的值.
的一个根,△ABC的三边a、b、c的长均为整数,试求a、b、c的值.
【答案】(1)②;(2)![]() ,
,![]() ;(3)a=2,b=3,c=2
;(3)a=2,b=3,c=2
【解析】
(1)先计算判别式的值得到△=b2+4ac,由于a、b、c为三角形的边长,则△>0,然后根据判别式的意义判断方程根的情况;
(2)连接OA,如图,根据垂径定理,由BD⊥AC得到,弧AB=弧CB,弧AD=弧CD,再利用圆心角、弧、弦的关系得到AB=CB,利用圆周角定理得到∠ABD=∠DAC=60°,则可判断△OAB为等边三角形,得到AB=OB=2,AE=![]() OB=
OB=![]() ,所以AC=2AE=2
,所以AC=2AE=2![]() ,即a=2,b=2
,即a=2,b=2![]() ,c-2,然后利用求根公式法解方程2x2+2
,c-2,然后利用求根公式法解方程2x2+2![]() x-2=0;
x-2=0;
(3)根据一元二次方程根的定义,把![]() 代入ax2+bx-c=0后变形得到
代入ax2+bx-c=0后变形得到![]() ,易得b<4,利用a、b、c的长均为整数得到b=1,2,3,然后分类讨论:当b=1时,ac=12,;当b=2时,ac=8;当b=3时,ac=4,再利用整数的整除性求出a、c的值,然后利用三角形三边的关系确定满足条件的a、b、c的值.
,易得b<4,利用a、b、c的长均为整数得到b=1,2,3,然后分类讨论:当b=1时,ac=12,;当b=2时,ac=8;当b=3时,ac=4,再利用整数的整除性求出a、c的值,然后利用三角形三边的关系确定满足条件的a、b、c的值.
(1)△=b2-4a(-c)=b+4ac,
∵a、b、c分别为∠A、∠B、∠C的对边,即a、b、c都是正数,
∴△>0,
∴方程有两个不相等的实数根;
故选②;
(2)连接OA,如图,
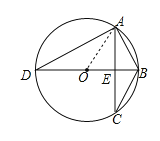
∵BD⊥AC,
∴弧AB=弧CB,弧AD=弧CD,
∴AB=CB,∠ABD=∠DAC=60°,
∴△OAB为等边三角形,
∴AB=OB=2,
∴AE=![]() OB=
OB=![]()
∴AC=2AE=![]() ,
,
即a=2,b=![]() ,c=2,
,c=2,
方程![]() 变形为
变形为![]() ,
,
整理得:,
解得![]() ,
,![]() ;
;
(3)把![]() 代入
代入![]() 得:
得:![]()
整理得:![]() ,则4-b>0,
,则4-b>0,
即b<4,
∵a、b、c的长均为整数,
∴b=1,2,3,
当b=1时,ac=12,则a=1,c=12;a=2,c=6;a=3,c=4;a=6,c=2;a=12,c=1,都不符合三角形三边的关系,舍去;
当b=2时,ac=8,则a=1,c=8;a=2,c=4;a=4,c=2;a=8,c=1,都不符合三角形三边的关系,舍去;
当b=3时,ac=4,则a=1,c=4;a=2,c=2;a=4,c=1,其中a=2,c=2符合三角形三边的关系,
∴a=2,b=3,c=2.