题目内容
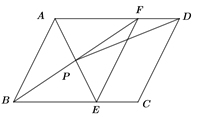
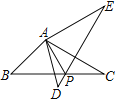
【题目】问题背景:如图,将![]() 绕点
绕点![]() 逆时针旋转60°得到
逆时针旋转60°得到![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,可推出结论:
,可推出结论:![]()
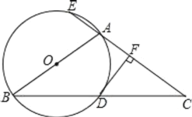
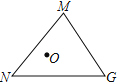
问题解决:如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 是
是![]() 内一点,则点
内一点,则点![]() 到
到![]() 三个顶点的距离和的最小值是___________
三个顶点的距离和的最小值是___________
【答案】![]()
【解析】
如图,将△MOG绕点M逆时针旋转60°,得到△MPQ,易知△MOP为等边三角形,继而得到点O到三顶点的距离为:ON+OM+OG=ON+OP+PQ,由此可以发现当点N、O、P、Q在同一条直线上时,有ON+OM+OG最小,此时,∠NMQ=75°+60°=135°,过Q作QA⊥NM交NM的延长线于A,利用勾股定理进行求解即可得.
如图,将△MOG绕点M逆时针旋转60°,得到△MPQ,
显然△MOP为等边三角形,
∴,OM+OG=OP+PQ,
∴点O到三顶点的距离为:ON+OM+OG=ON+OP+PQ,
∴当点N、O、P、Q在同一条直线上时,有ON+OM+OG最小,
此时,∠NMQ=75°+60°=135°,
过Q作QA⊥NM交NM的延长线于A,则∠MAQ=90°,
∴∠AMQ=180°-∠NMQ=45°,
∵MQ=MG=4![]() ,
,
∴AQ=AM=MQcos45°=4,
∴NQ=![]() ,
,
故答案为:![]() .
.


练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目