题目内容
【题目】如图,已知抛物线y=-x2+bx+c与一直线相交于A(-1,0),C(2,3)两点,与y轴交于点N.其顶点为D.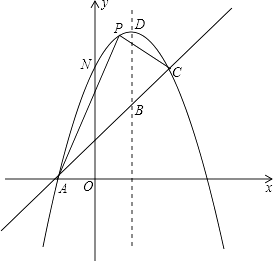
(1)抛物线及直线AC的函数关系式;
(2)设点M(3,m),求使MN+MD的值最小时m的值;
(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;
(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.
【答案】
(1)解:由抛物线y=-x2+bx+c过点A(-1,0)及C(2,3)得,
![]() ,
,
解得 ![]() ,
,
故抛物线为y=-x2+2x+3
又设直线为y=kx+n过点A(-1,0)及C(2,3)得
![]() ,
,
解得 ![]()
故直线AC为y=x+1
(2)解:如图1,作N点关于直线x=3的对称点N′,则N′(6,3),由(1)得D(1,4),
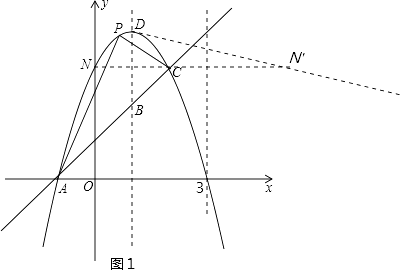
故直线DN′的函数关系式为y=- ![]() x+
x+ ![]() ,
,
当M(3,m)在直线DN′上时,MN+MD的值最小,
则m=- ![]() ×3+
×3+ ![]() =
= ![]()
(3)解:由(1)、(2)得D(1,4),B(1,2),
∵点E在直线AC上,
设E(x,x+1),
①当点E在线段AC上时,点F在点E上方,
则F(x,x+3),
∵F在抛物线上,
∴x+3=-x2+2x+3,
解得,x=0或x=1(舍去)
∴E(0,1);
②当点E在线段AC(或CA)延长线上时,点F在点E下方,
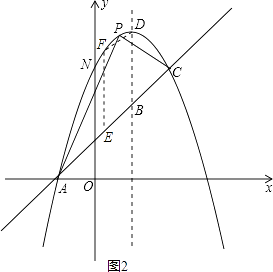
则F(x,x-1)
由F在抛物线上
∴x-1=-x2+2x+3
解得x= ![]() 或x=
或x= ![]()
∴E( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() )
)
综上,满足条件的点E的坐标为(0,1)、( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() )
)
(4)解:如图3,过点P作PQ⊥x轴交AC于点Q,交x轴于点H;过点C作CG⊥x轴于点G,
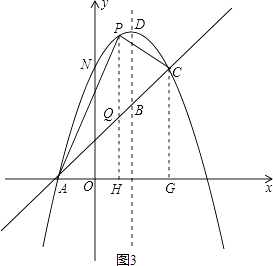
设Q(x,x+1),则P(x,-x2+2x+3)
∴PQ=(-x2+2x+3)-(x+1)
=-x2+x+2
又∵S△APC=S△APQ+S△CPQ
= ![]() PQAG
PQAG
= ![]() (-x2+x+2)×3
(-x2+x+2)×3
=- ![]() (x-
(x- ![]() )2+
)2+ ![]()
∴面积的最大值为 ![]()
【解析】(1)由A,C两点的坐标,用待定系数法求出抛物线和直线AC的函数关系式;(2)由使MN+MD的值最小,得到当M(3,m)在直线DN′上时,MN+MD的值最小,求出m的值;(3)由(1)、(2)得到D,B的坐标,由点E在直线AC上,求出点E的坐标;当点E在线段AC(或CA)延长线上时,点F在点E下方,由F在抛物线上,求出点E的坐标;(4)根据题意得到PQ的代数式,由三角形的面积公式S△APC=S△APQ+S△CPQ= ![]() PQAG,求出△APC的面积的最大值;此题是综合题,难度较大,计算和解方程时需认真仔细.
PQAG,求出△APC的面积的最大值;此题是综合题,难度较大,计算和解方程时需认真仔细.

 字词句段篇系列答案
字词句段篇系列答案


