题目内容
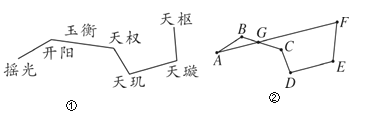
【题目】在平面直角坐标系中,横、纵坐标都为整数的点称为整点.如图,从内向外依次为第![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 个正方形(实线),若整点
个正方形(实线),若整点![]() 在第
在第![]() 个正方形的边上,则
个正方形的边上,则![]() ,
,![]() ,
,![]() 之间满足的数量关系为_______.
之间满足的数量关系为_______.

【答案】![]()
【解析】
解这道题时,先分别探究第1个正方形上的4个整点的坐标,第2个正方形上的8个整点的坐标,第3个正方形上的12个整点的坐标彼此之间的关系,进而可总结得到n与a和b之间的规律,问题自然解决.
解:由图可知,第1个正方形四条边上的格点共有4个,
它们的坐标分别为:(1,0),(0,1),(﹣1,0),(0,﹣1),
且这4个点的横纵坐标的绝对值之和为1;
第2个正方形四条边上的格点共有8个,
它们的坐标分别为:(2,0),(1,1),(0,2),(﹣1,1),(﹣2,0),(﹣1,﹣1),(0,﹣2),(1,﹣1),
且这8个点的横纵坐标的绝对值之和为2;
第3个正方形四条边上的格点共有12个,
它们的坐标分别为:(3,0),(2,1),(1,2),(0,3),(﹣1,2),(﹣2,1),(﹣3,0),(﹣2,﹣1),(﹣1,﹣2),(0,﹣3),(1,﹣2),(2,﹣1),
且这12个点的横纵坐标的绝对值之和为3;
由此可知:若整点![]() 在第
在第![]() 个正方形的边上,则
个正方形的边上,则![]() ,
,![]() ,
,![]() 之间满足的数量关系为
之间满足的数量关系为![]() ,
,
故答案为:![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为加强爱国主义教育,提高思想道德素质,某中学决定组织部分班级去山西国民师范旧址革命活动纪念馆开展红色旅游活动,在参加此次活动的师生中,若每位教师带17名学生,还剩12名学生没人带;若每位教师带18名学生,就有一位教师少带4名学生.现有甲、乙两种大客车,两种客车的载客量和租金如下表所示.
类别 | 甲种客车 | 乙种客车 |
载客量(人/辆) | 30 | 42 |
租金(元/辆) | 300 | 420 |
(1)参加此次红色旅游活动的教师和学生各有多少人?
(2)为了安全,每辆客车上要有2名教师.则怎样租车可以保证师生均有车坐,而且每辆车上都没有空座,也不超载,此时租车的费用为多少元?