题目内容
【题目】如图,将矩形ABCD沿EF折叠,使点C恰好落在AB边的中点C'上,点D落在D'处,C'D'交AE于点M.若AB=6,BC=9,求线段ED.

【答案】ED=3
【解析】
连接C'E,设DE=D'E=x,则AE=9-x,利用两次勾股定理分别表示出C'E2,进而得到方程求解即可.
解;如图,连接C'E,
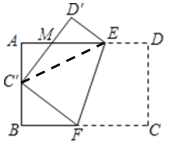
设DE=D'E=x,
∵在矩形ABCD中,AB=6,BC=9,
∴CD=AB=6,AD=BC=9,∠A=∠D=90°,
∴AE=AD-DE=9-x,
∵折叠,
∴∠D'=∠D=90°,C'D'=CD=6,
∵点C'为AB边的中点,
∴AC'=![]() AB=3,
AB=3,
在Rt△AEC'中,C'E2=AE2+AC'2=32+(9-x)2,
在Rt△C'D'E中,C'E2=C'D'2+D'E2=62+x2,
∴32+(9-x)2=62+x2,
解得x=3,
∴线段ED的长为3.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目