Question

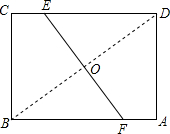如图，在矩形ABCD中，AB=16，BC=12，若将矩形折叠，使B点与D点重合，则折痕EF的长为

15

．

Answer 1

分析：根据勾股定理求出BD，求出BO，根据折叠得出OD=OB，∠EOB=90°，推出DE=BE，设DE=BE=x，根据勾股定理求出DE，再根据勾股定理求出OE即可．

解答：解：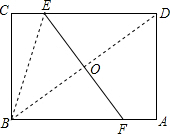
连接BE，
∵将矩形折叠，使B点与D点重合，
∴OB=OD，∠EOB=90°，
∴DE=BE，
设BE=DE=x，
∵四边形ABCD是矩形，
∴CD=AB=16，∠C=90°，
在Rt△BCD中，由勾股定理得：BD=

BC2+CD2

=

122+162

=20，
∴BO=10，
在Rt△BCE中，由勾股定理得：BC²+CE²=BE²，
即12²+（16-x）²=x²，
解得：x=

25

2

，
即BE=

25

2

，
在Rt△BEO中，由勾股定理得：EO=

( 25 2 )2-102

=

15

2

，
∵四边形ABCD是正方形，
∴DC∥AB，
∴△DOE∽△BOF，
∴

EO

OF

=

DO

BO

=

1

1

，
∴EO=OF，
即EF=2OE=2×

15

2

=15，
故答案为：15．

点评：本题考查了折叠的性质，线段垂直平分线性质，正方形性质，相似三角形的性质和判定的应用，主要考查学生的推理和计算能力．