题目内容
【题目】已知n（n≥3，且n为整数）条直线中只有两条直线平行，且任何三条直线都不交于同一个点．如图，当n=3时，共有2个交点；当n=4时，共有5个交点；当n=5时，共有9个交点；…依此规律，当共有交点个数为27时，则n的值为（ ）
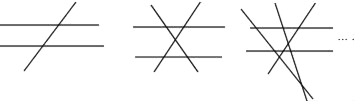
A. 6 B. 7 C. 8 D. 9
【答案】C
【解析】分析：首先通过观察图形，找到交点个数与直线条数之间的关系式，然后根据交点个数为27，列出关于n的方程，解方程求出n的值即可．
详解：∵当n3时，每增加一条直线，交点的个数就增加n1.即：
当n=3时，共有2个交点；
当n=4时,共有5个交点；
当n=5时,共有9个交点；
…，
∴n条直线共有交点2+3+4+…+(n1)=
个.
解方程=27,得n=8或7(负值舍去).
练习册系列答案
津桥教育计算小状元系列答案
相关题目
