题目内容
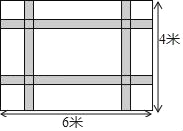
【题目】如图，一块长6米宽4米的地毯，为了美观设计了两横两纵的配色条纹（图中阴影部分），已知配色条纹的宽度相同，所占面积是整个地毯面积的
．
（1）求配色条纹的宽度；
（2）如果地毯配色条纹部分每平方米造价200元，其余部分每平方米造价100元，求地毯的总造价．（供参考数据：1052=11025，1152=13225，1252=15625）
【答案】（1）
米（2）2784元
【解析】【试题分析】（1）根据所占面积是整个地毯面积的
列出方程，即可；（2）直接计算地毯配色条纹部分总造价加上其余部分的总造价即可.
【试题解析】
（1）设配色条纹的宽度为x米，
根据题意得：2×6x+2×4x﹣4x2=
×6×4，
整理得：25x2﹣125x+24=0，
解得：x1=
（不符合题意，舍去），x2=
．
答：配色条纹的宽度为米．
（2）地毯总造价为：×6×4×200+（1﹣）×4×6×100=2784（元）．
答：地毯的总造价为2784元．
练习册系列答案
相关题目
【题目】现在电器进入销售旺季，福清某电器超市销售每台进价分别为
元、
元的
两种型号的电器，下表是近两周的销售情况：（进价、售价均保持不变，利润=销售收入-进货成本）
销售时段 | 销售数量 | 销售收入 | |
|
| ||
第一周 |
|
|
|
第二周 |
|
|
|
（1）求两种型号的电器销售单价；
（2）若超市准备用不超过
元的金额再采购这种型号的电器共台，销售完这台电器实现利润超过
元的目标，请给出相应的采购方案；并求出利润的最大值.
