题目内容
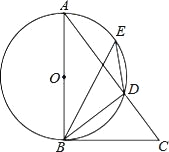
【题目】如图,AB是⊙O的直径,点E是![]() 上的一点,∠DBC=∠BED.
上的一点,∠DBC=∠BED.
(1)请判断直线BC与⊙O的位置关系,并说明理由;
(2)已知AD=5,CD=4,求BC的长.
【答案】(1)BC与![]() 相切;理由见解析;
相切;理由见解析;
(2)BC=6
【解析】
试题(1)BC与![]() 相切;由已知可得∠BAD=∠BED又由∠DBC=∠BED可得∠BAD=∠DBC,由AB为直径可得∠ADB=90°,从而可得∠CBO=90°,继而可得BC与
相切;由已知可得∠BAD=∠BED又由∠DBC=∠BED可得∠BAD=∠DBC,由AB为直径可得∠ADB=90°,从而可得∠CBO=90°,继而可得BC与![]() 相切
相切
(2)由AB为直径可得∠ADB=90°,从而可得∠BDC=90°,由BC与![]() 相切,可得∠CBO=90°,从而可得∠BDC=∠CBO,可得
相切,可得∠CBO=90°,从而可得∠BDC=∠CBO,可得![]() ,所以得
,所以得![]() ,得
,得![]() ,由
,由![]() 可得AC=9,从而可得BC=6(BC="-6" 舍去)
可得AC=9,从而可得BC=6(BC="-6" 舍去)
试题解析:(1)BC与![]() 相切;
相切;
∵![]() ,∴∠BAD=∠BED ,∵∠DBC=∠BED,∴∠BAD=∠DBC,∵AB为直径,∴∠ADB=90°,∴∠BAD+∠ABD=90°,∴∠DBC+∠ABD=90°,∴∠CBO=90°,∴点B在
,∴∠BAD=∠BED ,∵∠DBC=∠BED,∴∠BAD=∠DBC,∵AB为直径,∴∠ADB=90°,∴∠BAD+∠ABD=90°,∴∠DBC+∠ABD=90°,∴∠CBO=90°,∴点B在![]() 上,∴BC与
上,∴BC与![]() 相切
相切
(2)∵AB为直径,∴∠ADB=90°,∴∠BDC=90°,∵BC与![]() 相切,∴∠CBO=90°,∴∠BDC=∠CBO,∴
相切,∴∠CBO=90°,∴∠BDC=∠CBO,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∵
,∵![]() ,∴AC=9,∴
,∴AC=9,∴![]() ,∴BC=6(BC="-6" 舍去)
,∴BC=6(BC="-6" 舍去)

练习册系列答案
相关题目
【题目】甲、乙两人参加射击比赛,两人成绩如图所示.
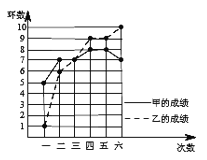
(1)填表:
平均数 | 方差 | 中位数 | 众数 | |
甲 | 7 | 1 | 7 | |
乙 | 9 |
(2)只看平均数和方差,成绩更好的是 .(填“甲”或“乙”)
(3)仅就折线图上两人射击命中环数的走势看,更有潜力的是 .(填“甲”或“乙”)